問題
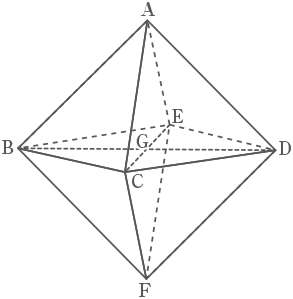
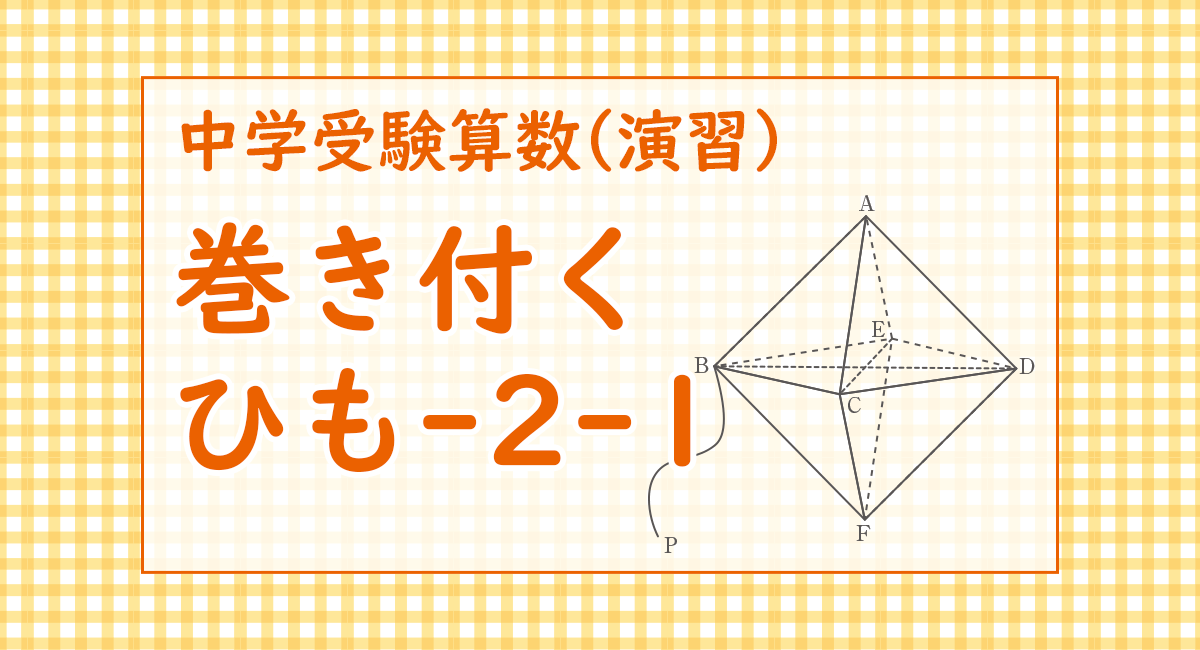
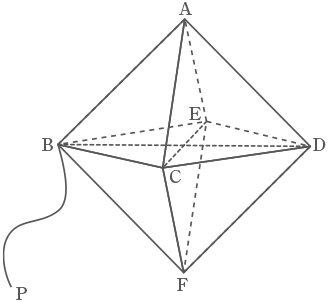
右の図のような、大きさの等しい正三角形を八つ合わせてできる立体ABCDEFがあります。BDの長さは4cmです。頂点Bに、この立体の1辺と等しい長さのひもの先端をつけました。
このとき、次の問いに答えなさい。
(1)この立体の体積を求めなさい。
(2)この立体の表面上で、ひものもう一方の先端(せんたん)Pが届く範囲の面積を求めなさい。
ただし、円周率は3.14とし、答えは小数第3位を四捨五入して小数第2位まで求めなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
右の図のような、大きさの等しい正三角形を八つ合わせてできる立体ABCDEFがあります。BDの長さは4cmです。頂点Bに、この立体の1辺と等しい長さのひもの先端をつけました。
このとき、次の問いに答えなさい。(1)この立体の体積を求めなさい。
(2)この立体の表面上で、ひものもう一方の先端(せんたん)Pが届く範囲の面積を求めなさい。
ただし、円周率は3.14とし、答えは小数第3位を四捨五入して小数第2位まで求めなさい。

(1)
平面BCDEは正方形であり、その対角線同士の交わる点をGとする。点Gから立体の各頂点A~Fまでの距離は全て等しい。この立体は正八面体であり、その特徴が分かれば(1)は解ける。
四角すいA-BCDEの体積の2倍が求める体積となる。
正方形BCDEの面積=4×4÷2=8cm2
高さAG=2cm
四角すいA-BCDEの体積=8×2÷3=$ \displaystyle \frac{16}{3} $
求める立体の体積=$ \displaystyle \frac{16}{3} $×2=$ \displaystyle \frac{32}{3} $=10$ \displaystyle \frac{2}{3} $(答え) 10$ \displaystyle \frac{2}{3} $cm3
(2)

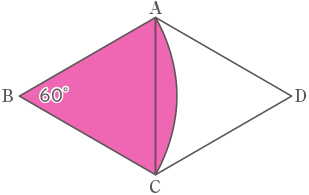
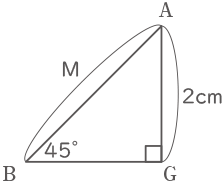
8面のうち、図の2面だけに着目して平面で考えると、ひもの届く範囲は中心角60°のおうぎ形になる。

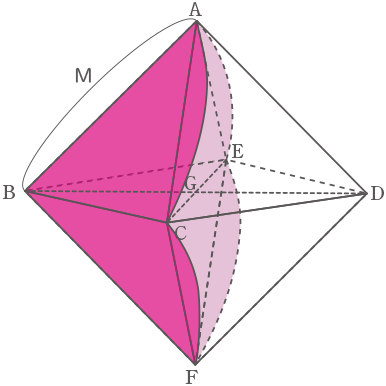
8面全てでは、ひもの届く範囲は図の様になり、辺ABの長さをMとすれば求める面積は、
M×M×3.14×$ \displaystyle \frac{60}{360} $×4となる。・・・(ア) Mの長さを知りたいが小学校の範囲では直角二等辺三角形のMの長さは求められない。だが、(ア)の式に含まれるM×Mであれば面積として求められ、この方法を使った問題はよく見かける。
Mの長さを知りたいが小学校の範囲では直角二等辺三角形のMの長さは求められない。だが、(ア)の式に含まれるM×Mであれば面積として求められ、この方法を使った問題はよく見かける。M×Mで求められる面積は、三角形ABGの面積の4倍なので、
M×M=(2×2÷2)×4=8とわかり、(ア)の式に当てはめれば、
8×3.14×$ \displaystyle \frac{60}{360} $×4=16.7$\cancel{4}\cancel{6}$・・・=16.75(答え) 16.75cm2