問題
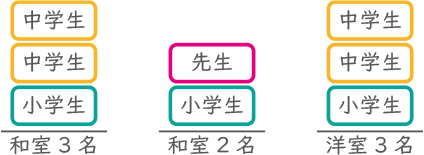
先生1人,中学生4人,小学生3人の合計8人で,合宿に出かけました。合宿先では,定員が3名の和室,定員が2名の和室,定員が3名の洋室を1室ずつ借りて,分かれて泊まることになりました。ただし,先生は必ず和室に泊まり,小学生3人は1人ずつ分かれて泊まることにします。
8人の泊まり方は全部で何通りありますか。答えだけでなく,途中の考え方も書きなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
先生1人,中学生4人,小学生3人の合計8人で,合宿に出かけました。合宿先では,定員が3名の和室,定員が2名の和室,定員が3名の洋室を1室ずつ借りて,分かれて泊まることになりました。ただし,先生は必ず和室に泊まり,小学生3人は1人ずつ分かれて泊まることにします。
8人の泊まり方は全部で何通りありますか。答えだけでなく,途中の考え方も書きなさい。先生が2名用和室に泊まる場合

【小学生の泊まり方】
まず、和室3名には3人のうち誰でもいいので3通り。
次に、和室2名には残り2人のうち誰でもいいので2通り。
最後に、洋室3名には残りの1人なので1通り。
よって、3×2×1=6通り。(順列)
【中学生の泊まり方】
4人のうちの2人の選び方は、$ \displaystyle \frac{4×3}{2×1} $=6通り。(組み合わせ)
全員では6×6=36通り。先生が3名用和室に泊まる場合

【小学生の泊まり方】
前述と同じ数え方で6通り。(順列)
【中学生の泊まり方】
まず、和室3名には4人のうち誰でもいいので4通り。
次に、和室2名には残り3人のうち誰でもいいので3通り。
最後に、洋室3名には残りの2人なので1通り。
よって、4×3×1=12通り。(順列)
全員では6×12=72通り。あわせて36+72=108通り。
(答え) 108通り