問題
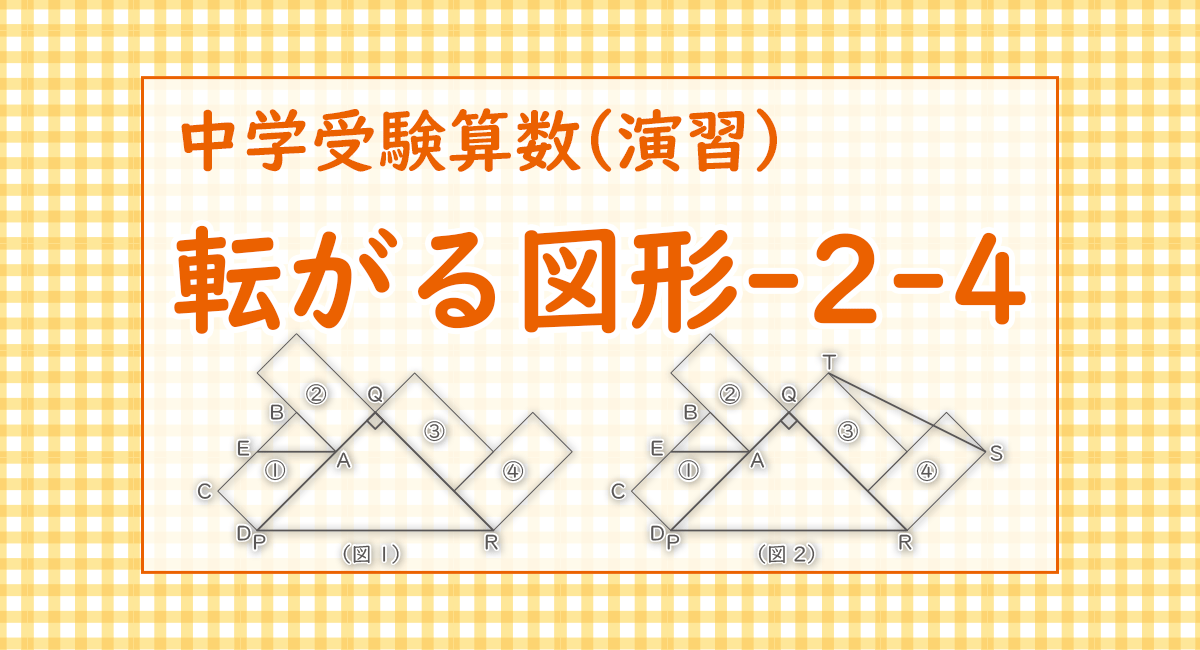
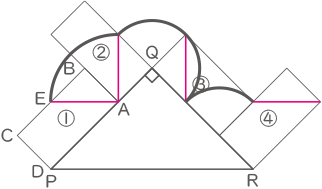
下の( 図1)のようなPQ=QR=3cmの直角二等辺三角形PQRがあり、2辺PQ,QR上を、2辺の長さが1cm, 2cmの長方形ABCDが①から④の状態まですべることなく転がっていきます。また、BCの真ん中の点をEとします。(円周率は3.14)
(1) ①から④の状態になるまでにEが動いた道のりを、解答用紙の図の中にかきなさい。
(2) ①から②の状態になるまでにAEが通ってできる図形の面積は何cm2ですか。
(3) ②から③の状態になるまでにAEが通ってできる図形の面積は何cm2ですか。
(4) 下の(図2)のように、③,④の長方形の頂点をそれぞれT,Sとします。次の(ア)、(イ)に答えなさい。
(ア) 四角形QRSTの面積は何cm2ですか。
(イ) ③から④の状態になるまでにAEが通ってできる図形の面積は何cm2ですか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
下の( 図1)のようなPQ=QR=3cmの直角二等辺三角形PQRがあり、2辺PQ,QR上を、2辺の長さが1cm, 2cmの長方形ABCDが①から④の状態まですべることなく転がっていきます。また、BCの真ん中の点をEとします。(円周率は3.14)
(1) ①から④の状態になるまでにEが動いた道のりを、解答用紙の図の中にかきなさい。
(2) ①から②の状態になるまでにAEが通ってできる図形の面積は何cm2ですか。
(3) ②から③の状態になるまでにAEが通ってできる図形の面積は何cm2ですか。
(4) 下の(図2)のように、③,④の長方形の頂点をそれぞれT,Sとします。次の(ア)、(イ)に答えなさい。
(ア) 四角形QRSTの面積は何cm2ですか。
(イ) ③から④の状態になるまでにAEが通ってできる図形の面積は何cm2ですか。

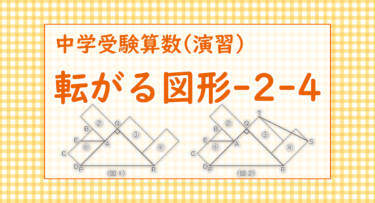
(1)
(答え)

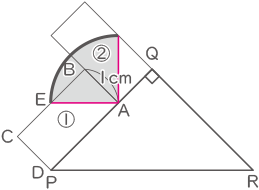
 (2)
(2)
1×1×2×3.14×$ \displaystyle \frac{1}{4} $=1.57cm2詳しい解き方はここを参照【正方形の面積(半径×半径)が分かっている場合に円の面積を求める問題】
(答え) 1.57cm2
(3)
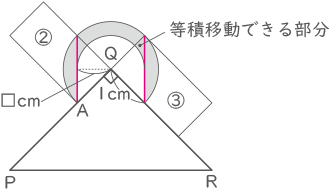
等積移動できる部分があるので、
1×1×3.14×$ \displaystyle \frac{3}{4} $-□×□×3.14×$ \displaystyle \frac{1}{2} $-1×1×$ \displaystyle \frac{1}{2} $が求める面積の式
□×□は面積として求められるので1×1×$ \displaystyle \frac{1}{2} $=$ \displaystyle \frac{1}{2} $
よって、
1×1×3.14×$ \displaystyle \frac{3}{4} $-$ \displaystyle \frac{1}{2} $×3.14×$ \displaystyle \frac{1}{2} $-1×1×$ \displaystyle \frac{1}{2} $=1.57-0.5=1.07
(答え) 1.07cm2
(4)―(ア)
求める面積の図形は台形。
(1+2)×3÷2=4.5(答え) 4.5cm2
(4)―(イ)
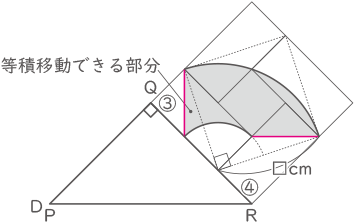
求める面積の図形はその一部を等積移動すると扇形となる。
(□×□-1×1)×3.14×$ \displaystyle \frac{1}{4} $が求める面積の式
□×□は図より、5cm2
よって、
(5-1×1)×3.14×$ \displaystyle \frac{1}{4} $=3.14cm2
(答え) 3.14cm2

 (2)
(2)