問題
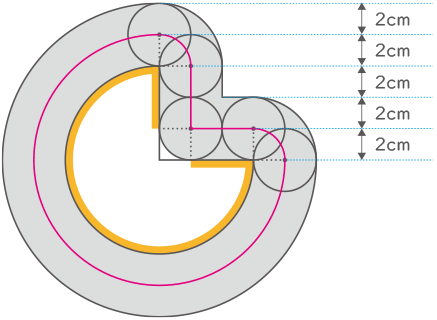
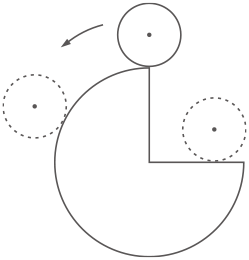
半径6cm, 中心角270゜のおうぎ形があります。下の図のように,半径2cmの円が,おうぎ形の周りを矢印の方向におうぎ形に接しながら1周して,元の位置に戻ります。
次の□に当てはまる数を求めなさい。(円周率は3.14とします。)
(1) おうぎ形の周のうち,円と接することができる部分の長さは□cmです。
(2) 円の中心が動いてできる線の長さは□cmです。
(3) 円が通ったあとにできる図形の面積は□cm2です。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
半径6cm, 中心角270゜のおうぎ形があります。下の図のように,半径2cmの円が,おうぎ形の周りを矢印の方向におうぎ形に接しながら1周して,元の位置に戻ります。
次の□に当てはまる数を求めなさい。(円周率は3.14とします。)
(1) おうぎ形の周のうち,円と接することができる部分の長さは□cmです。
(2) 円の中心が動いてできる線の長さは□cmです。
(3) 円が通ったあとにできる図形の面積は□cm2です。

(1)
黄色線が、円と接することができる部分の長さなので、6×2×3.14×$ \displaystyle \frac{270}{360} $+4+4=36.26(答え) 36.26cm
(2)
赤線が、円の中心が動いてできる線の長さで、半径8cmと半径2cmの円の一部と直線からなるので、8×2×3.14×$ \displaystyle \frac{270}{360} $+2×2×3.14×$ \displaystyle \frac{90}{360} $×2+4+4=51.96
(答え) 51.96cm
(3)
灰色の色の付いている部分が、円が通ったあとにできる図形の面積。
【解法1】:(2)で求めた長さを使い<縦×横>で求める方法
【解法2】:全体の面積から穴あき部分を引く方法【解法1】
4cm・・・縦と見立てる
×(51.96-2-2)cm・・・横と見立てる(半径2cmの円の高さ「縦」が通ったところ以外は抜かす)
+2cm×2cm×3つ・・・直角に曲がるところに1辺2cmの正方形が3つ
+2cm×2cm×3.14×$ \displaystyle \frac{1}{4} $・・・半径2cmの円の4分の1円
=206.98【解法2】
10cm×10cm×3.14×$ \displaystyle \frac{3}{4} $・・・半径10cmの円の4分の3円
+4cm×4cm×3.14×$ \displaystyle \frac{1}{4} $×2・・・半径4cmの円の4分の1円が2つ
+2cm×2cm×8・・・直角に曲がるところに1辺2cmの正方形が8つ
-6cm×6cm×3.14×$ \displaystyle \frac{3}{4} $・・・穴あき部分(半径6cmの円の4分の3円)
-(2cm×2cm-2cm×2cm×3.14×$ \displaystyle \frac{1}{4} $)・・・穴あき部分(半径2cmの円の角)
=206.98(答え) 206.98cm2