問題
問題(麻布中学2011/円の動ける範囲、普段から作図は丁寧に)
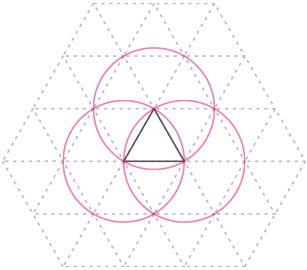
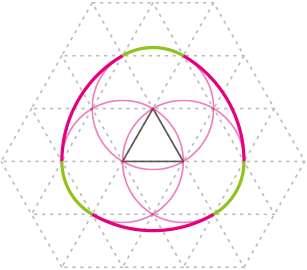
図1のように,一辺が1cmの正三角形を底面とする三角柱が平面の上に固定されていて,半径1cmの円形の輪が,三角柱が内部にくるように平面上に置かれています。
この輪を平面上で動かすことを考えます。図2は輪が動く様子を真上から見たものです。
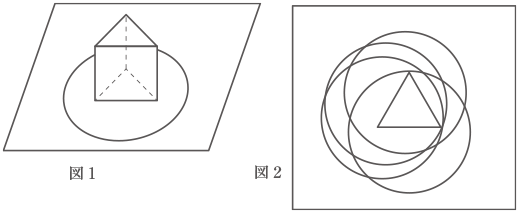
(1) 輪が動けるところをすべて動いたとき,輪が通過した剖分を,図中に境界となる線をかいたうえで斜線で示しなさい。ただし,太線の正三角形を三角柱の底面とします。
(2) (1)で答えた部分の面積を求めなさい。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
図1のように,一辺が1cmの正三角形を底面とする三角柱が平面の上に固定されていて,半径1cmの円形の輪が,三角柱が内部にくるように平面上に置かれています。
この輪を平面上で動かすことを考えます。図2は輪が動く様子を真上から見たものです。
(1) 輪が動けるところをすべて動いたとき,輪が通過した剖分を,図中に境界となる線をかいたうえで斜線で示しなさい。ただし,太線の正三角形を三角柱の底面とします。

(2) (1)で答えた部分の面積を求めなさい。
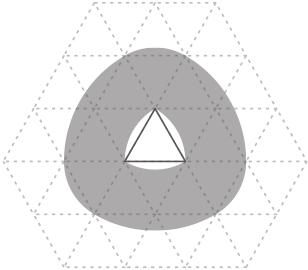
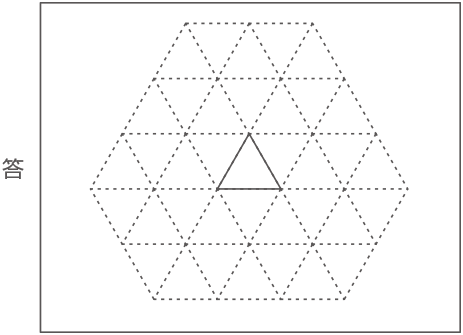
(1)

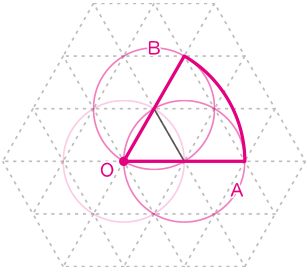
正三角形の3辺にピッタリ寄せた場合に図の様になる。

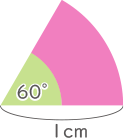
点Oを回転の中心として円A,Bの間の動く範囲を考えると、図の様なおうぎ形ができる。

半径1cmと半径2cmの円の弧の一部で外側の境界線が出来ている。

(答え) 図の色の付いた部分が斜線で示すところ。
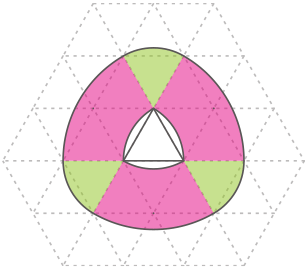
(2)


図の様に等積移動すると、
求める面積=2×2×3.14×$ \displaystyle \frac{60}{360} $×3=6.28(答え) 6.28cm2
ではまた~