問題
問題(逗子開成中学2022/分かり易い例を作って考えましょう)
連続した47個の整数があります。これらの整数を偶数と奇数の2つのグループに分け,それぞれのグループの和を求めました。これらの差が46であるとき,この47個の整数の中で,もっとも小さい整数はいくつですか。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
連続した47個の整数があります。これらの整数を偶数と奇数の2つのグループに分け,それぞれのグループの和を求めました。これらの差が46であるとき,この47個の整数の中で,もっとも小さい整数はいくつですか。
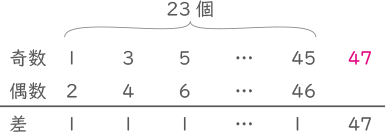
1~47までの数で考える。

47-23で差は24だが、この差を46にしたい。
□-23=46となる□は69
このときのもっとも小さい整数は1+(69-47)で23。(なお、偶数の整数が多い場合でもおなじ。)
(答え) 23
ではまた~