問題
問題（渋谷教育学園渋谷中学2022/難しさはないですが面倒くさいですね・・・）
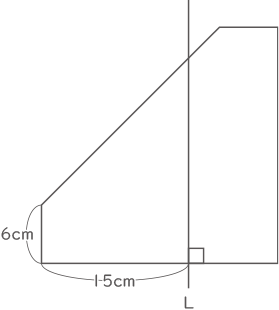右の図は1辺24cmの正方形から，直角二等辺三角形を取り除いた図形です。この図形を直線Lを軸として1回転させてできる立体の体積は何cm3ですか。
ただし，円周率は3.14とします。また，すい体の体積は「（底面積）×（高さ）÷3」で求めることができます。
【家庭学習】過去問をA３で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
右の図は1辺24cmの正方形から，直角二等辺三角形を取り除いた図形です。この図形を直線Lを軸として1回転させてできる立体の体積は何cm3ですか。
ただし，円周率は3.14とします。また，すい体の体積は「（底面積）×（高さ）÷3」で求めることができます。
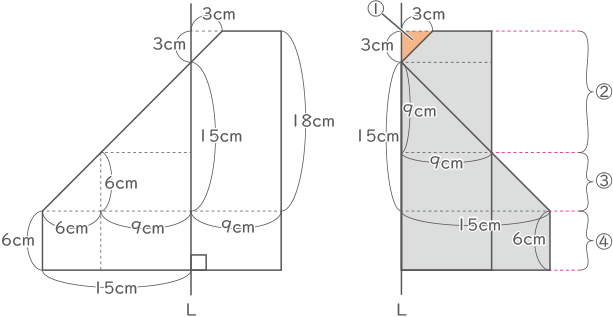
①を回転させた三角すいの体積は
3×3×3.14×3×$ \displaystyle \frac{1}{3} $＝（9×3.14）cm3・・・他の三角すいの体積はこれをもとに比で求める②を回転させた体積
9×9×3.14×12－9×3.14＝（963×3.14）cm3③を回転させた体積（相似な立体の比が使えるので①を利用）
9×3.14×（5×5×5－3×3×3）=（882×3.14）cm3④を回転させた体積
15×15×3.14×6＝（1350×3.14）cm3合わせて、
963×3.14＋882×3.14＋1350×3.14＝10032.3cm3（答え） 10032.3cm3
ではまた～
