問題
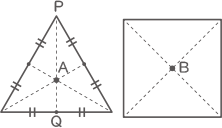 右の図のように、正三角形のそれぞれの辺の真ん中の点と頂点を結ぶ直線は3本引くことができます。この3本は1点Aで交わり、PA:AQ =2:1となります。
右の図のように、正三角形のそれぞれの辺の真ん中の点と頂点を結ぶ直線は3本引くことができます。この3本は1点Aで交わり、PA:AQ =2:1となります。
また、正方形の2本の対角線の交わる点をBとします。このような2つの点A、Bをそれぞれ「正三角形の中心」「正方形の中心」と呼ぶことにします。
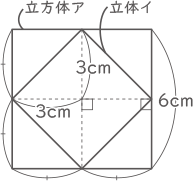
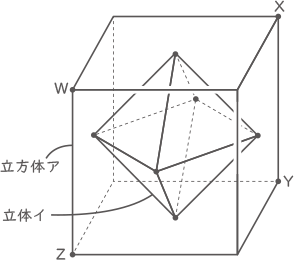 (1) 図のように、1辺の長さが6cmの立方体アのそれぞれの面の中心を頂点とする立体イを考えます。このとき、立体イの体積は、立方体アの体積の何倍ですか。
(1) 図のように、1辺の長さが6cmの立方体アのそれぞれの面の中心を頂点とする立体イを考えます。このとき、立体イの体積は、立方体アの体積の何倍ですか。
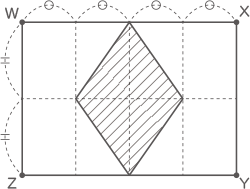
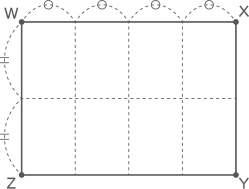 (2) (1)の図について、立方体アと立体イを、点W,X,Y,Zを通る平面で切断しました。次の図は、立方体アの断面図です。この図の中に立体イの切断面を、斜線をつけてかきなさい。
(2) (1)の図について、立方体アと立体イを、点W,X,Y,Zを通る平面で切断しました。次の図は、立方体アの断面図です。この図の中に立体イの切断面を、斜線をつけてかきなさい。
(3) 立方体アの頂点Wと頂点Yをまっすぐに結んだ直線は、立体イの2つの面と交わります。この2つの面と交わる点を、Wに近いほうをS、Yに近いほうをTとします。STの長さとWYの長さの比を求めなさい。
立体イには8つの面があり、すべて正三角形です。この立体イのそれぞれの面の中心を頂点とする立体ウを考えます。
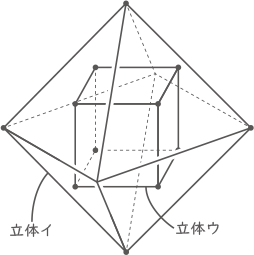
(4) 立体ウの体積は、立方体アの体積の何倍ですか。
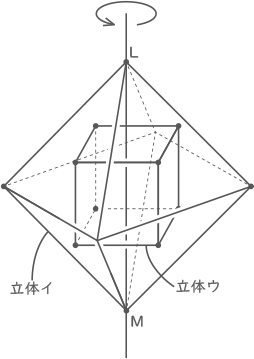 (5) 右の図のように、立体イと立体ウを直線LMを軸として1回転させました。立体イが回転してできる立体の体積は、立体ウが回転してできる立体の体積の何倍ですか。
(5) 右の図のように、立体イと立体ウを直線LMを軸として1回転させました。立体イが回転してできる立体の体積は、立体ウが回転してできる立体の体積の何倍ですか。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
 右の図のように、正三角形のそれぞれの辺の真ん中の点と頂点を結ぶ直線は3本引くことができます。この3本は1点Aで交わり、PA:AQ =2:1となります。
右の図のように、正三角形のそれぞれの辺の真ん中の点と頂点を結ぶ直線は3本引くことができます。この3本は1点Aで交わり、PA:AQ =2:1となります。
また、正方形の2本の対角線の交わる点をBとします。このような2つの点A、Bをそれぞれ「正三角形の中心」「正方形の中心」と呼ぶことにします。 (1) 図のように、1辺の長さが6cmの立方体アのそれぞれの面の中心を頂点とする立体イを考えます。このとき、立体イの体積は、立方体アの体積の何倍ですか。
(1) 図のように、1辺の長さが6cmの立方体アのそれぞれの面の中心を頂点とする立体イを考えます。このとき、立体イの体積は、立方体アの体積の何倍ですか。 (2) (1)の図について、立方体アと立体イを、点W,X,Y,Zを通る平面で切断しました。次の図は、立方体アの断面図です。この図の中に立体イの切断面を、斜線をつけてかきなさい。
(2) (1)の図について、立方体アと立体イを、点W,X,Y,Zを通る平面で切断しました。次の図は、立方体アの断面図です。この図の中に立体イの切断面を、斜線をつけてかきなさい。(3) 立方体アの頂点Wと頂点Yをまっすぐに結んだ直線は、立体イの2つの面と交わります。この2つの面と交わる点を、Wに近いほうをS、Yに近いほうをTとします。STの長さとWYの長さの比を求めなさい。
立体イには8つの面があり、すべて正三角形です。この立体イのそれぞれの面の中心を頂点とする立体ウを考えます。

(4) 立体ウの体積は、立方体アの体積の何倍ですか。
 (5) 右の図のように、立体イと立体ウを直線LMを軸として1回転させました。立体イが回転してできる立体の体積は、立体ウが回転してできる立体の体積の何倍ですか。
(5) 右の図のように、立体イと立体ウを直線LMを軸として1回転させました。立体イが回転してできる立体の体積は、立体ウが回転してできる立体の体積の何倍ですか。 (1)
(1)
(立体イは正八面体)
どの面から見ても図のように見える。
立方体アの体積は、6×6×6=216cm3
立体イの体積は、6×6×$ \displaystyle \frac{1}{2} $×3×$ \displaystyle \frac{1}{3} $×2=36cm3
36÷216=$ \displaystyle \frac{1}{6} $(答え) $ \displaystyle \frac{1}{6} $倍
 (2)
(2)
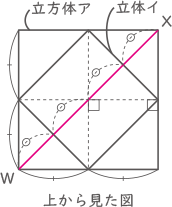
(1)の図がヒント、赤線が切断面を上から見たところ。(答え)

 (3)
(3)
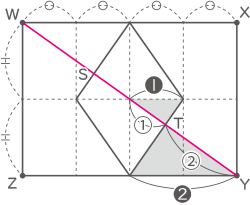
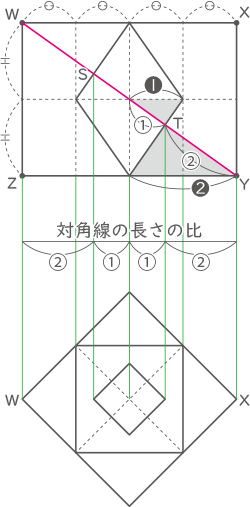
(2)の答えの図を利用し、相似な三角形の比から図の様な比となるので、ST:WY=②:⑥=1:3。(答え) 1:3
 (4)
(4)
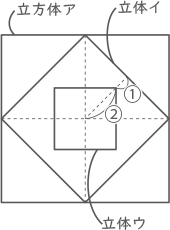
(立体ウは立方体)
図は外側の立方体の各面から見たもので、どの面から見ても同じ。また、問題文の「PA:AQ =2:1」のことより、図の様に①:②の比となる。 (3)の答えの図と平面から見た図を合わせると、大小の立方体の平面で見た対角線の長さが、②:⑥=1:3の比であることがかわる。
(3)の答えの図と平面から見た図を合わせると、大小の立方体の平面で見た対角線の長さが、②:⑥=1:3の比であることがかわる。
よって、1辺の長さの比も同じことより、体積比は1×1×1:3×3×3=1:27となる。
立体ウの体積は、立方体アの体積の$ \displaystyle \frac{1}{27} $倍。(答え) $ \displaystyle \frac{1}{27} $倍
 (5)
(5)
前問で求まった比を入れ、立体イで作られる上下の円すいの半径は△とする。
立体イが回転してできる立体の体積は、
△×△×3.14×❸×$ \displaystyle \frac{1}{3} $(❸にしているので円すい2つ分)
立体ウが回転してできる立体の体積は、
②×②×3.14×❶
ここで、△×△=③×③×2より、
立体イで作られる立体の体積:立体ウで作られる立体の体積
=③×③×2×3.14×❸×$ \displaystyle \frac{1}{3} $:②×②×3.14×❶
=⑱×❶:④×❶
=⑨:②
立体イが回転してできる立体の体積は、立体ウが回転してできる立体の体積の$ \displaystyle \frac{9}{2} $倍。(答え) $ \displaystyle \frac{9}{2} $倍 (4.5倍)


 (1)
(1) (2)
(2)
 (3)
(3) (4)
(4) (3)の答えの図と平面から見た図を合わせると、大小の立方体の平面で見た対角線の長さが、②:⑥=1:3の比であることがかわる。
(3)の答えの図と平面から見た図を合わせると、大小の立方体の平面で見た対角線の長さが、②:⑥=1:3の比であることがかわる。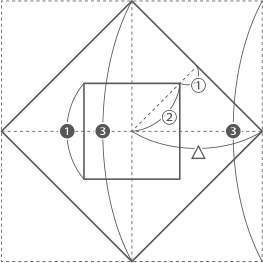 (5)
(5)








