問題
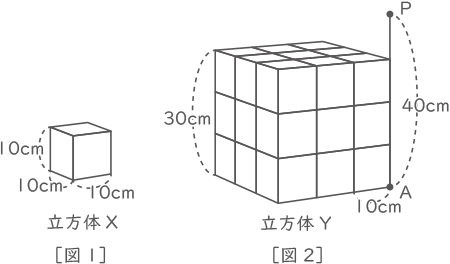
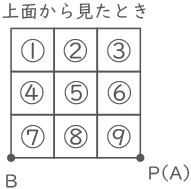
[図1]のような1辺の長さが10cmの立方休Xを27個用意し、これを[図2]のように平らな床(ゆか)の上に積み重ねて1辺の長さが30cmの立方体Yを作りました。そして、立方体Yの頂点Aの真上40cmのところにある電球Pでこの立方体を照らしました。このとき、後の問いに答えなさい。ただし、電球Pはすべての方向を照らすものとし、電球の大きさは考えないものとします。
(1) 電球Pによって床の上にできる立方体Yの影(かげ)の面積は何cm2ですか。
以下、[ ア ] ~ [ エ ]にあてはまる数をそれぞれ求めなさい。
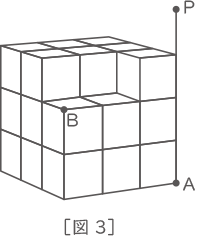
(2) [図2]の立方体Yの上段から立方体Xを2個取り除いた[図3]のような立休を作り、[図2]と同じ場所にある電球Pによってこの立体を照らしました。このとき、床の上にできる点Bの影は、点Aから[ ア ]cmのところにあります。また、床の上にできるこの立体の影の面積は、(1)で求めた影の面積よりも[ イ ]cm2小さくなります。
(3) [図2]の立方体Yの上段には立方体Xが全部で9個あります。このうち1つだけを取り除いてできる9種類の立休に対して、それぞれ[図2]と同じ場所にある電球Pによって立体を照らし、床の上にできる影の面積を考えます。このとき床の上にできる影の面積は、大きさが同じものを1通りと考えると全部で[ ウ ]通りあり、そのうち面積が最大のものと最小のものの差は[ エ ]cm2となります。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
[図1]のような1辺の長さが10cmの立方休Xを27個用意し、これを[図2]のように平らな床(ゆか)の上に積み重ねて1辺の長さが30cmの立方体Yを作りました。そして、立方体Yの頂点Aの真上40cmのところにある電球Pでこの立方体を照らしました。このとき、後の問いに答えなさい。ただし、電球Pはすべての方向を照らすものとし、電球の大きさは考えないものとします。

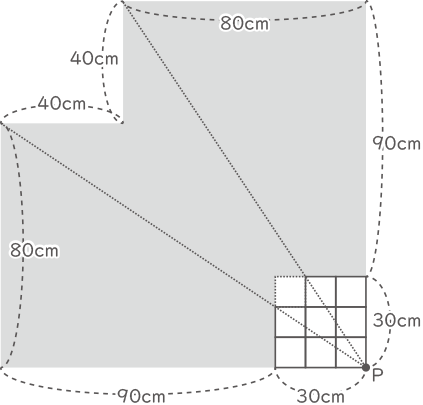
(1) 電球Pによって床の上にできる立方体Yの影(かげ)の面積は何cm2ですか。
以下、[ ア ] ~ [ エ ]にあてはまる数をそれぞれ求めなさい。
(2) [図2]の立方体Yの上段から立方体Xを2個取り除いた[図3]のような立休を作り、[図2]と同じ場所にある電球Pによってこの立体を照らしました。このとき、床の上にできる点Bの影は、点Aから[ ア ]cmのところにあります。また、床の上にできるこの立体の影の面積は、(1)で求めた影の面積よりも[ イ ]cm2小さくなります。

(3) [図2]の立方体Yの上段には立方体Xが全部で9個あります。このうち1つだけを取り除いてできる9種類の立休に対して、それぞれ[図2]と同じ場所にある電球Pによって立体を照らし、床の上にできる影の面積を考えます。このとき床の上にできる影の面積は、大きさが同じものを1通りと考えると全部で[ ウ ]通りあり、そのうち面積が最大のものと最小のものの差は[ エ ]cm2となります。
(1)
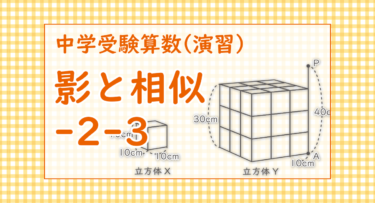
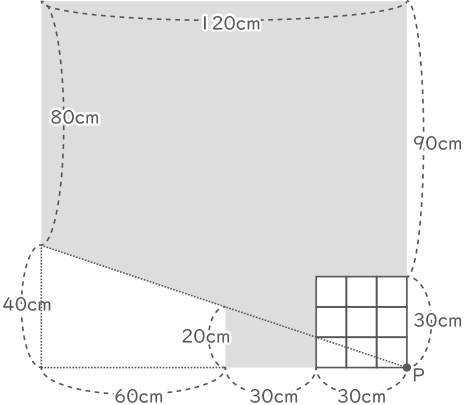
横から見たとき。
三角形の相似より、10:30=40:□、□=120cm
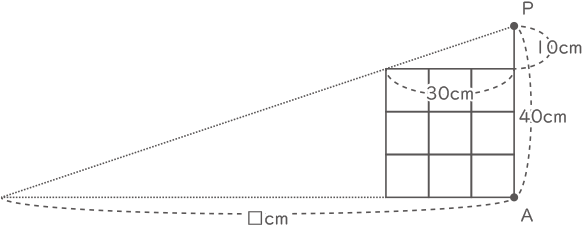
上から影を見たとき。

120×120-30×30=13500cm2
(答え) 13500cm2
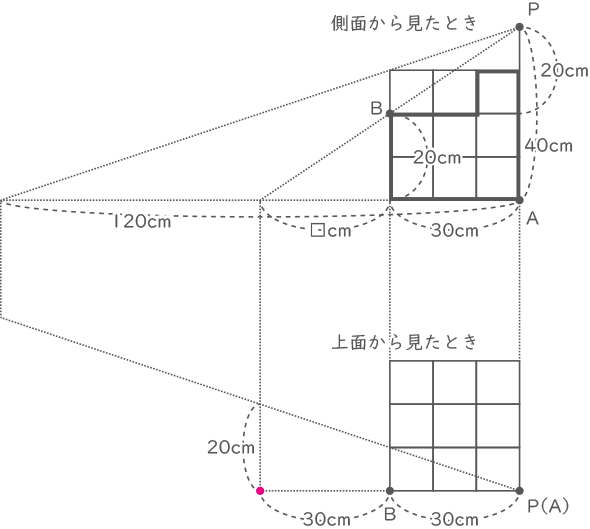
(2)-ア
三角形の相似より、□=30cm
点Bの影は、点Aから60cmのところにある。
(答え) 60
(2)-イ
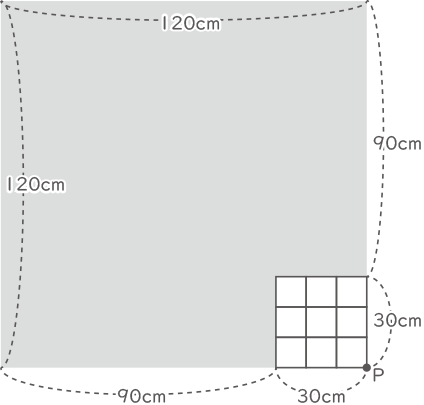
(2)-アの図より、上から見た影は下図のようになる。
影が減った部分の形は台形なので、(20+40)×60÷2=1800cm2
(答え) 1800
 (2)-ウ
(2)-ウ
⑤、⑥、⑧、⑨は(1)の解答の影と同じで、影に変化はない。
③と⑦は同じ影の面積。
②と④は同じ影の面積。
①だけ他の影の面積と異なる。
よって、影は4通り。(答え) 4
(2)-エ
①の影が一番遠くまで伸びるので、①を除くと影が最小になる。
また、影が最大になるのは(1)の影の形状のとき。
①を除いたことで減った影の面積は、40×40=1600cm2で、これが最大のものと最小のものの差となる。
(答え) 1600


 (2)-ウ
(2)-ウ