問題
台形の形をしたテーブルがあり,図1のようにこのテーブル2台の1番長い辺どうしをつけると正六角形が作れます。
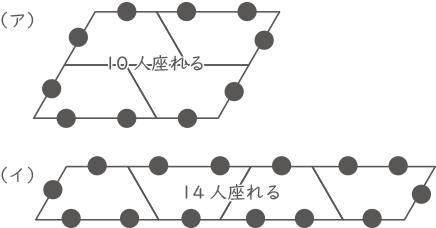
体育館に集まった小学生が,このテーブルをすべて並べて全員で着席します。テーブルの周りには, 1つの辺について80cmあたりに1人座ることができます。テーブルを4台使って図2の(ア)のような平行四辺形を作って並べると,テーブルは余ることなく平行四辺形ができ,12人が座ることができませんでした。(イ)のような平行四辺形を作って並べると,(ア)と同じ個数の平行四辺形ができ,40人分の席が余ります。
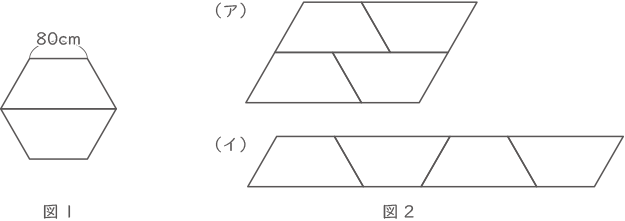
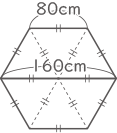
(1) 1台の台形のテーブルについて,1番長い辺の長さは何cmですか。解答用紙の図を利用し,理由もつけて答えなさい。
(2) 台形のテーブルは何台ありますか。また,集まった小学生は何人ですか。
(3) テーブルを3台使って正三角形を作ることができます。テーブルをすべて使って,この正三角形と図2の(ア)の平行四辺形をそれぞれ何個かずつ作ったところ,席を余らせることなくちょうど全員座ることができました。
① テーブルを3台使って正三角形を1つ作ると何人座ることができますか。
② 正三角形を何個作りましたか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
台形の形をしたテーブルがあり,図1のようにこのテーブル2台の1番長い辺どうしをつけると正六角形が作れます。
体育館に集まった小学生が,このテーブルをすべて並べて全員で着席します。テーブルの周りには, 1つの辺について80cmあたりに1人座ることができます。テーブルを4台使って図2の(ア)のような平行四辺形を作って並べると,テーブルは余ることなく平行四辺形ができ,12人が座ることができませんでした。(イ)のような平行四辺形を作って並べると,(ア)と同じ個数の平行四辺形ができ,40人分の席が余ります。
(1) 1台の台形のテーブルについて,1番長い辺の長さは何cmですか。解答用紙の図を利用し,理由もつけて答えなさい。
(2) 台形のテーブルは何台ありますか。また,集まった小学生は何人ですか。
(3) テーブルを3台使って正三角形を作ることができます。テーブルをすべて使って,この正三角形と図2の(ア)の平行四辺形をそれぞれ何個かずつ作ったところ,席を余らせることなくちょうど全員座ることができました。
① テーブルを3台使って正三角形を1つ作ると何人座ることができますか。
② 正三角形を何個作りましたか。(1)

(答え) (理由) 図の様に補助線を引くと、大きさの同じ6個の正三角形が出来るので、1番長い辺の長さは160cmです。
(2)
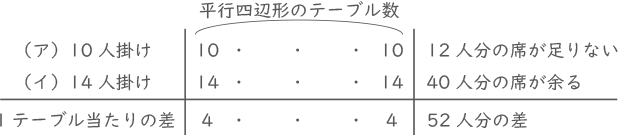
(ア)では10人座れ、(イ)では14人座れる。

1テーブル当たり4人分の差があり、その集まりが52人分になる。
52÷4=13
平行四辺形のテーブルは13あり、台形のテーブルは13×4=52台。
小学生の数は、10×13+12=142人。(答え) 台形のテーブルは52台 小学生は142人
 (3)-①
(3)-①
図の通りで9人。(答え) 9人
(3)-②
平行四辺形のテーブル1つにつき10人座れる。
正三角形のテーブル1つにつき9人座れる。
人数142人の下一桁2は9×8=72で作れるので正三角形のテーブルが8つ必要になる。(答え)
(以下はその確かめ)
残りの台形テーブルは52-3×8=28台なので、平行四辺形のテーブルは28÷4=7つ作れる。
正三角形のテーブル8つに座れる人数は9×8=72人
平行四辺形のテーブル7つに座れる人数は10×7=70人
合わせて72+70=142人、人数もちょうどよい。(答え) 8個

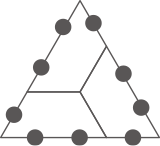 (3)-①
(3)-①