問題
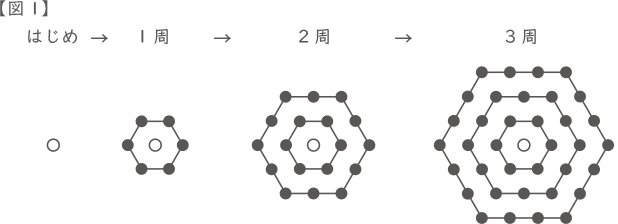
【図1】のように，はじめに白石を1個置きます。次に，1周，2 周，…と，はじめの白石を正六角形で囲むように黒石を置いていきます。
次の各問いに答えなさい。
（1） はじめの白石をちょうど10周まで黒石で囲むために必要な石の総数は，はじめの白石を含めて何個ですか。
（2） 黒石の総数が1000個のとき，はじめの白石を最大で何周まで黒石で囲むことができますか。
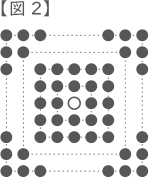（3） まず，【図1】のように，はじめの白石をちょうど□周まで囲むように黒石を置きました。次に，そこで用いた黒石をすべて使って，【図2】のように，はじめの白石を正方形で囲むように置き直したところ，ちょうど何周かの正方形で囲むことができました。□に入る最も小さい数を求めなさい。
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 ＜オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます！しかも授業料は【格安】＞
解答
- 解答を開く
-
【図1】のように，はじめに白石を1個置きます。次に，1周，2 周，…と，はじめの白石を正六角形で囲むように黒石を置いていきます。
次の各問いに答えなさい。（1） はじめの白石をちょうど10周まで黒石で囲むために必要な石の総数は，はじめの白石を含めて何個ですか。
（2） 黒石の総数が1000個のとき，はじめの白石を最大で何周まで黒石で囲むことができますか。
（3） まず，【図1】のように，はじめの白石をちょうど□周まで囲むように黒石を置きました。次に，そこで用いた黒石をすべて使って，【図2】のように，はじめの白石を正方形で囲むように置き直したところ，ちょうど何周かの正方形で囲むことができました。□に入る最も小さい数を求めなさい。（1）
1周の総数：1＋6×1
2周の総数：1＋6×1＋6×2
3周の総数：1＋6×1＋6×2＋6×3
・・・
10周の総数：1＋6×1＋6×2＋…＋6×10=1＋6×（1＋10）×10÷2＝331（答え） 331個
（2）
問（1）の10周の総数と同じように式をつくると、
●周の総数：1＋6×1＋6×2＋…＋6×●・・・これが1000に近くなる●を求める。
1＋6×（1＋●）×●÷2＝1000
（1＋●）×●＝333
18×17＝306
19×18＝342
●は17が当てはまり、17周まで黒石で囲むことができる。（答え） 17周
（3）
【図2】の▲周の総数を求める。
1周の総数：1＋2×4
2周の総数：1＋2×4＋4×4
3周の総数：1＋2×4＋4×4＋6×4
・・・
▲周の総数：1＋2×4＋4×4＋…＋（▲×2）×41＋2×4＋4×4＋…＋（▲×2）×4
＝1＋｛（1＋2＋…＋▲）×2｝×4
＝1＋（1＋▲）×▲×4、この式が問（2）で使った式
1＋6×（1＋□）×□÷2＝1＋（1＋□）×□×3と等しくなる□と▲を見つける。1＋（1＋□）×□×3=1＋（1＋▲）×▲×4
（1＋□）×□×3=（1＋▲）×▲×4 ⇐ □に数字を入れてゆく□＝1のとき、2×1×3・・・不適切
□＝2のとき、3×2×3・・・不適切
□＝3のとき、4×3×3・・・不適切
□＝4のとき、5×4×3・・・不適切
□＝5のとき、6×5×3・・・不適切
□＝6のとき、7×6×3・・・不適切
□＝7のとき、8×7×3=7×6×4・・・形が合う
よって、7周。（答え） 7
