問題
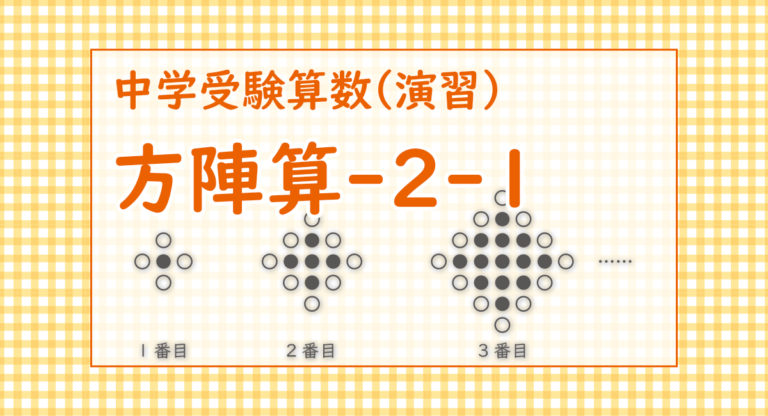
図のように,〇と●の碁(ご)石が一定の規則で並んでいます。
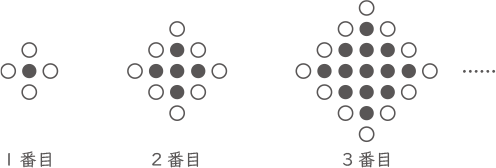
次の問いに答えなさい。
(1) 4番目の〇の碁石は何個ありますか。
(2) 9番目の●の碁石は何個ありますか。
(3) ●の碁石が初めて2021個より多くなるのは何番目ですか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
図のように,〇と●の碁(ご)石が一定の規則で並んでいます。

次の問いに答えなさい。
(1) 4番目の〇の碁石は何個ありますか。
(2) 9番目の●の碁石は何個ありますか。
(3) ●の碁石が初めて2021個より多くなるのは何番目ですか。(1)
1番目:辺の個数は2
2番目:辺の個数は3
3番目:辺の個数は4
4番目:辺の個数は5で〇の碁石の数は5×2+3×2=16個(答え) 16個
(2)
9番目の●の碁石の個数は8番目の全碁石の個数と同じ。
1番目:碁石の個数は1+4
2番目:碁石の個数は1+4+8
3番目:碁石の個数は1+4+8+12
4番目:碁石の個数は1+4+8+12+16
…
8番目:碁石の個数は1+4+8+12+16+…+32=1+4×(1+2+3+…+8)=145個。(答え) 145個
(3)
□番目:碁石の個数は1+4+8+12+16+…+□×4=1+4×(1+2+3+…+□)
2021から半端な1は除き、2020÷4=505から、1+2+3+…+□が505に近い数字を探す。
(1+□)×□×$ \displaystyle \frac{1}{2} $が505に近くなる
(1+□)×□が1010に近くなる
31×32=992
32×33=1056
□が32のとき、すなわち32番目のときに全碁石の個数が2021個を超え、●の個数が2021個を超えるのは33番目のとき。(答え) 33番目