速さ-2-5（吉祥女子中学2022/これが解ければ比・逆比がよく理解出来ている。なお、大問の中の小問なので使える時間は5分もない）

問題

解答

 解答を開く

 

A地点から、B地点を通ってC地点まで行くとき、B地点までは毎分80mで歩き、そのあとは毎分200mで走ると、ちょうど6分かかります。また、B地点までは毎分200mで走り、そのあとは毎分80mで歩くと、6分36秒かかります。A地点からC地点までの道のりは何mですか。

 

---

 

【進み方１】　［A］―毎分80m―［B］―毎分200m―［C］
【進み方２】　［A］―毎分200m―［B］―毎分80m―［C］
とする。

AB=BCであれば進み方による時間の差は出ない。
長い距離を遅く進む方が時間が掛かる　→　BCの方がABより長い

そこで、BC間にAB＝BXとなるX地点をとる。

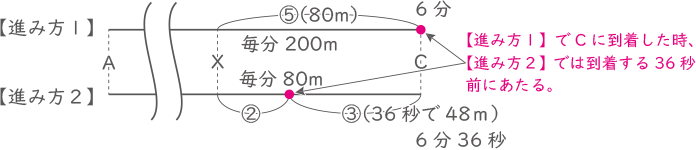
【進み方１】と【進み方２】では途中の位置は異なるが、X地点到着は同時。
その後、【進み方１】の方が先にC地点に到着し、36秒遅れて【進み方２】で到着する。

毎分80mでは36秒で48ｍ進む。
速さの比は、毎分200ｍ：毎分80ｍ＝⑤：②
よって、図の様に③＝48ｍとなり、XCの距離⑤＝80ｍとわかる。

ABとBXは同じ距離であり、同じ距離にかかる時間の比は先程の逆比で、毎分200ｍ：毎分80ｍより2⃣：5⃣

この事を【進み方２】で考える。

XCは80ｍで１分かかるので、AXは5分36秒＝5$ \displaystyle \frac{36}{60} $分
5$ \displaystyle \frac{36}{60} $分が7⃣のとき2⃣は$ \displaystyle \frac{336}{60} $×$ \displaystyle \frac{2}{7} $＝$ \displaystyle \frac{96}{60} $分

毎分200mで$ \displaystyle \frac{96}{60} $分走ると320ｍとなるので、A地点からC地点までの道のりは320×2＋80＝720ｍ。

（答え）　720ｍ