問題
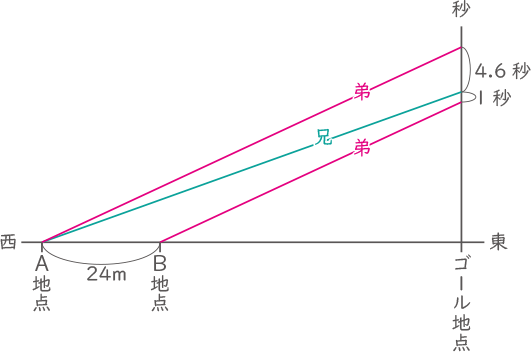
兄と弟の2人が,図のような東西にのびた道で,自転車に乗って競走します。2人はそれぞれ一定の速さで走リ,スタート地点を変えて何回か競走します。ただし,ゴール地点は毎回変わリません。
![]()
はじめに2回競走したところ,結果は次のようになりました。
● 2人がA地点から同時に出発したところ,兄が弟よリ4.6秒早くゴール地点に到着(とうちゃく)しました。
● A地点の24m東にB地点があリます。弟がB地点から,兄がA地点から同時に出発したところ,弟が兄より1秒早くゴール地点に到着しました。
(1) 弟の速さは秒速何mですか。
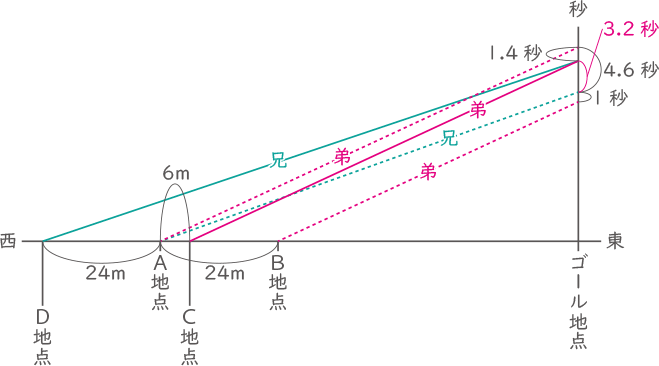
さらにもう1回競走したところ,結果は次のようになリました。
● A地点の6m東にC地点があり,A地点の24m西にD地点があリます。弟がC地点から,兄がD地点から同時に出発したところ, 2人は同時にゴール地点に到着しました。
(2) 兄の速さは秒速何mですか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
兄と弟の2人が,図のような東西にのびた道で,自転車に乗って競走します。2人はそれぞれ一定の速さで走リ,スタート地点を変えて何回か競走します。ただし,ゴール地点は毎回変わリません。

はじめに2回競走したところ,結果は次のようになりました。
● 2人がA地点から同時に出発したところ,兄が弟よリ4.6秒早くゴール地点に到着(とうちゃく)しました。
● A地点の24m東にB地点があリます。弟がB地点から,兄がA地点から同時に出発したところ,弟が兄より1秒早くゴール地点に到着しました。(1) 弟の速さは秒速何mですか。
さらにもう1回競走したところ,結果は次のようになリました。
● A地点の6m東にC地点があり,A地点の24m西にD地点があリます。弟がC地点から,兄がD地点から同時に出発したところ, 2人は同時にゴール地点に到着しました。
(2) 兄の速さは秒速何mですか。
(1)
弟は24m短いと5.6秒早くゴールするので24mを5.6秒で走るとわかる。
24÷5.6=4$ \displaystyle \frac{2}{7} $、弟の速さは秒速4$ \displaystyle \frac{2}{7} $m。
(答え) 秒速4$ \displaystyle \frac{2}{7} $m
(2)
弟の速さは秒速4$ \displaystyle \frac{2}{7} $mなので、A地点より6m短いC地点からは、6÷4$ \displaystyle \frac{2}{7} $=1.4秒早くゴール地点に着く。
兄をグラフで見ると、A地点から24m遠いD地点からでは4.6-1.4=3.2秒多く時間がかかるので、兄は24mを3.2秒で走るとわかる。
兄の速さは24÷3.2=7.5、秒速7.5m。
(答え) 秒速7.5m