問題
同じ高さまで水が入った2つの直方体の水そうがあります。2つの水そうの容積の比は9:32で,大きな水そうは小さな水そうの2倍の高さがあります。2つの水そうそれぞれに,さらに675mLずつ水を人れると,小さな水そうは全体の77%,大きな水そうは全体の28%まで水が入りました。大きな水そうにはじめから入っていた水の最は□mL です。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
同じ高さまで水が入った2つの直方体の水そうがあります。2つの水そうの容積の比は9:32で,大きな水そうは小さな水そうの2倍の高さがあります。2つの水そうそれぞれに,さらに675mLずつ水を人れると,小さな水そうは全体の77%,大きな水そうは全体の28%まで水が入りました。大きな水そうにはじめから入っていた水の最は□mL です。
計算を簡単にするために大きな容器の高さを半分で考える。

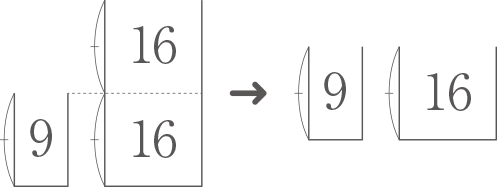
(ⅰ)高さが同じとき、大きな水そうの容量:小さな水そうの容量=16:9であれば、大きな水そうの底面積:小さな水そうの底面積=⑯:⑨
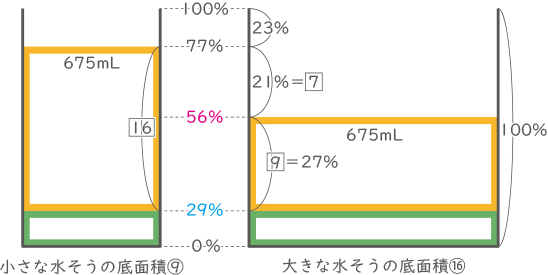
(ⅱ)大きな水そうの下半分だけで考えると、56%(28×2)まで水が入ったことになる。
(ⅲ)底面積比⑨:⑯より、675mLの水の高さは小:大=$ \fbox{16} $:$ \fbox{9} $となり、差が$ \fbox{7} $となる。
(ⅳ)高さの21%が$ \fbox{7} $にあたるので、$ \fbox{1} $が3%にあたり、$ \fbox{9} $は27%
(ⅴ)大きな水そうに始めから入っていた水の高さは100-23-21-27=29%
(ⅵ)675mLが27%にあたるので、29%は675×$ \displaystyle \frac{29}{27} $=725mL(答え) 725