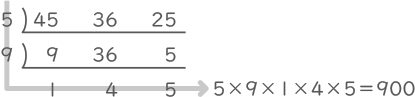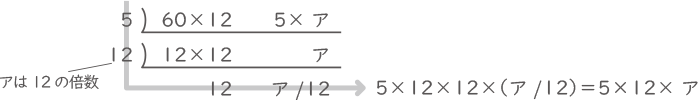最大公約数・最小公倍数-2-2（浅野中学2022/複数のメトロノームが同時に鳴るのは何秒後？）

1 問題
2 解答

問題

問題（複数のメトロノームが同時に鳴るのは何秒後？）

いくつかのメトロノームがあります。メトロノームとは、一定の時間ごとに音を鳴らし続けることができる音楽の練習用の器具です。1分間にA回の割合で音が鳴るメトロノームを【♪=A】で表すことにします。例えば、【♪=30】であれば、1分間に30回、すなわち2秒に1回のペースで音が鳴るということを表します。次の問いに答えなさい。

（1）【♪=80】と【♪=100】の2種類のメトロノームが1つずつあります。この2つのメトロノームの音が同時に鳴ったとき、次に音が同時に鳴るのは何秒後ですか。

（2）【♪=80】と【♪=100】と【♪=144】の3種類のメトロノームが1つずつあります。この3つのメトロノームの音が同時に鳴ったとき、次に3つの音が同時に鳴るのは何秒後ですか。

（3）【♪=［ア］】と【♪=144】の2種類のメトロノームが1つずつあり、【♪=［ア］】は【♪=144】よりもゆっくりとしたペースで音が嗚ります。この2つのメトロノームの音が同時に鳴ったとき、次に音が同時に鳴るのは5秒後です。このとき、［ア］にあてはまる整数をすべて答えなさい。ただし、答えが2つ以上になる場合は、「2、3」のように、答えと答えの間に「、」をつけなさい。

灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ！ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。

解答

解答を開く

（1）
【♪=80】は$ \displaystyle \frac{3}{4} $秒ごとに、【♪=100】は$ \displaystyle \frac{3}{5} $秒ごとに鳴る。
分母を最小公倍数で合わせると、
【♪=80】は$ \displaystyle \frac{15}{20} $秒ごと、【♪=100】は$ \displaystyle \frac{12}{20} $秒ごと。
分子の最小公倍数は、

【♪=80】と【♪=100】は$ \displaystyle \frac{60}{20} $＝3秒ごとに同時に鳴るので3秒後。

（答え）　3秒後

（2）
【♪=80】は$ \displaystyle \frac{3}{4} $秒ごと、【♪=100】は$ \displaystyle \frac{3}{5} $秒ごと、【♪=144】は$ \displaystyle \frac{5}{12} $秒ごとに鳴る。
分母を最小公倍数で合わせると、
【♪=80】は$ \displaystyle \frac{45}{60} $秒ごと、【♪=100】は$ \displaystyle \frac{36}{60} $秒ごと、【♪=144】は$ \displaystyle \frac{25}{60} $秒ごと。
分子の最小公倍数は、

【♪=80】と【♪=100】は$ \displaystyle \frac{900}{60} $＝15秒ごとに同時に鳴るので15秒後。

（答え）　15秒後

（3）
【♪=［ア］】が5秒間に1回鳴るのであればアは12（=12×1）、
【♪=［ア］】が5秒間に2回鳴るのであればアは24（=12×2）、
・・・
【♪=［ア］】が5秒間に11回鳴るのであればアは132（=12×11）、
【♪=144】よりもゆっくりなのでアは144未満。

【♪=［ア］】は$ \displaystyle \frac{60}{ア} $秒ごとに、【♪=144】は$ \displaystyle \frac{5}{12} $秒ごとに鳴る。
分母を公倍数で合わせると、
【♪=［ア］】は$ \displaystyle \frac{60×12}{ア×12} $秒ごと、【♪=144】は$ \displaystyle \frac{5×ア}{12×ア} $秒ごと。
分子の最小公倍数は、