問題
次の問いに答えなさい。ただし、円周率は3.14とします。
(1) 図1のような、底辺の長さ2cm,高さ6cmの直角三角形が4枚あります。これらを図2のように配置して、正方形ABCDを作りました。
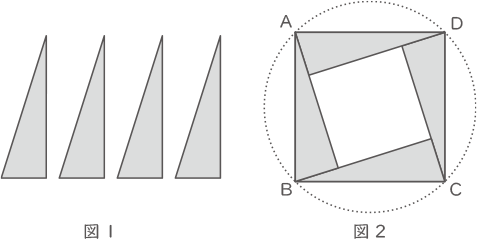
① 正方形ABCDの面積は何cm2ですか。
② 4点A,B,C,Dを通る円の面積は何cm2ですか
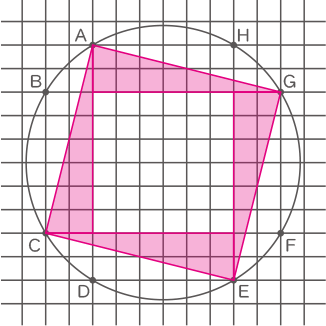
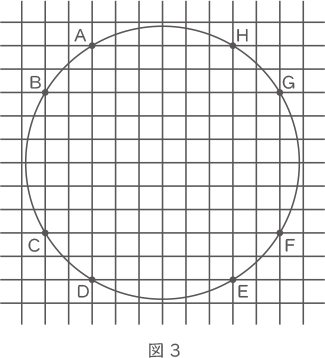
(2) 図3のように、縦方向と横方向それぞれに1cm間かくで直線が引かれている方眼に、円が描(か)かれています。この円は、縦の直線と横の直線が交わる点A,B,C,D,E,F,G,Hを通っています。この円の面積は何cm2ですか。
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 <オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます!しかも授業料は【格安】>
解答
- 解答を開く
-
次の問いに答えなさい。ただし、円周率は3.14とします。
(1) 図1のような、底辺の長さ2cm,高さ6cmの直角三角形が4枚あります。これらを図2のように配置して、正方形ABCDを作りました。

① 正方形ABCDの面積は何cm2ですか。
② 4点A,B,C,Dを通る円の面積は何cm2ですか(2) 図3のように、縦方向と横方向それぞれに1cm間かくで直線が引かれている方眼に、円が描(か)かれています。この円は、縦の直線と横の直線が交わる点A,B,C,D,E,F,G,Hを通っています。この円の面積は何cm2ですか。

(1)―①
直角三角形1つの面積=2×6÷2=6cm2
内側の正方形の面積=(6-2)×(6-2)=16cm2
正方形ABCDの面積=6×4+16=40cm2(答え) 40cm2
(1)―②
(円の半径×円の半径)は(1)―①の半分の20cm2なので20×3.14=62.8cm2(答え) 62.8cm2
(2)
(1)がヒントになっているので同じ手順で進める。
下図の様に直角三角形をつくり正方形の面積を求める。
直角三角形1つの面積=2×8÷2=8cm2
内側の正方形の面積=6×6=36cm2
正方形ACEGの面積=8×4+36=68cm2
円の面積=68÷2×3.14=106.76cm2(答え) 106.76cm2
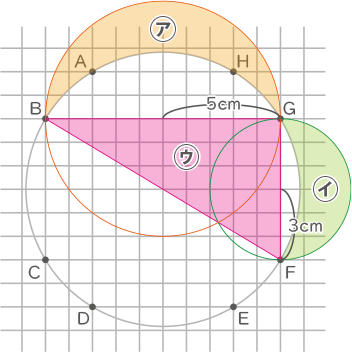
ヒポクラテスの三日月を使う手もある下図のようにヒポクラテスの三日月が出来る。
・㋒は1辺が大きな円の直径となる直角三角形
・㋐は㋒の1辺を直径とする円を弧に持つ
・㋑は㋒の他の1辺を直径とする円を弧に持つ
㋐+㋑=㋒となるので、
5×5×3.14+3×3×3.14=106.76cm2