問題
問題(複数の円と正方形の中心が同じとき)
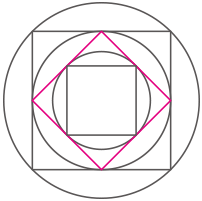
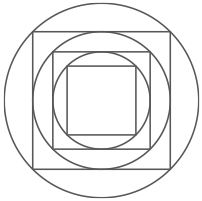
図の様に、3種類の大きさの円と正方形があり、正方形の2つの対角線の交点と円の中心は全て同じ位置にあります。1番大きな円の面積が56.52のとき、1番小さな正方形の周りの長さを求めなさい。ただし円周率は3.14とします。
自宅学習で身につける、難関中学への合格力「Z会」
4.02
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
図の様に、3種類の大きさの円と正方形があり、正方形の2つの対角線の交点と円の中心は全て同じ位置にあります。1番大きな円の面積が56.52のとき、1番小さな正方形の周りの長さを求めなさい。ただし円周率は3.14とします。


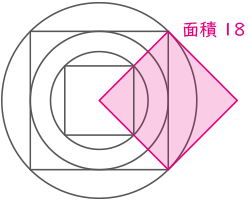
図の様に、2番目に大きい正方形を回転させると、2番目に大きい正方形は1番小さい正方形の倍の面積とわかり、1番大きい正方形は2番目に大きい正方形の倍の面積とわかる。よって、1番大きい正方形は1番小さい正方形の4倍の面積で、倍の辺の長さとわかる。

1番大きい円の面積が56.52なので、その(半径×半径)は56.52÷3.14=18となり、これは2番目に大きい正方形の面積と同じ。よって、1番大きい正方形については面積が18×2=36で1辺の長さは6となる。
1番小さな正方形の1辺の長さは3で周りの長さは3×4=12。
(答え) 12
ではまた~