問題
問題(渋谷教育学園幕張中学2022/5つの円を組み合わせてできた図形について、よく見かける問題)
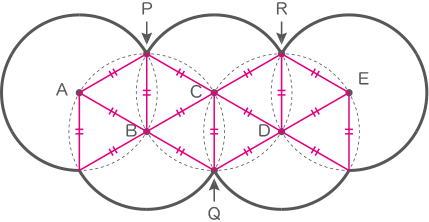
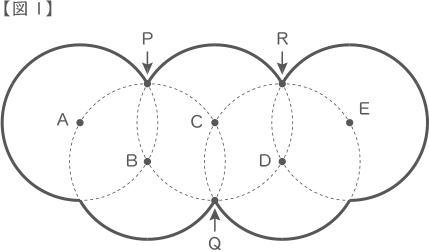
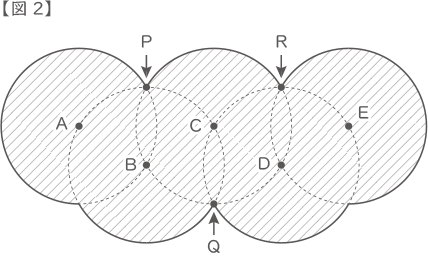
【図1】のように,半径3cmの円5つを組み合わせてできた太線の図形を考えます。
5つの円の中心A,B,C,D,Eは,すべてとなりの円の周上にあります。
また,点P,Q,Rは3つの円が1点で交わっている点です。
円周率を3.14として,次の各問いに答えなさい。
(1) 太線の長さは何cmですか。
(2) 【図2】の斜線部分(図1の太線で囲まれた部分)の面積は何cm2ですか。ただし,1辺の長さが3cmの正三角形の面積は3.9cm2とします。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
【図1】のように,半径3cmの円5つを組み合わせてできた太線の図形を考えます。
5つの円の中心A,B,C,D,Eは,すべてとなりの円の周上にあります。
また,点P,Q,Rは3つの円が1点で交わっている点です。
円周率を3.14として,次の各問いに答えなさい。(1) 太線の長さは何cmですか。

(2) 【図2】の斜線部分(図1の太線で囲まれた部分)の面積は何cm2ですか。ただし,1辺の長さが3cmの正三角形の面積は3.9cm2とします。

(1)
3×2×3.14×$ \displaystyle \frac{1}{360} $×(240+120+240+120+120)=43.96cm
(答え) 43.96cm
(2)
図形は複数のおうぎ形と1辺の長さが3cmの正三角形8個で作られている。
3×3×3.14×$ \displaystyle \frac{1}{360} $×(240+120+240+120+120)+3.9×8=97.14cm2
(答え) 97.14cm2
ではまた~