問題
問題（逗子開成中学2022/これもよく見かける問題、式をこねくり回すとうまくいくパターン）
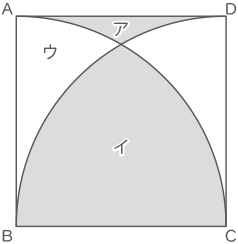
下の図は，1辺8cmの正方形ABCDに点Bと点Cを中心とし正方形の1辺を半径として2個のおうぎ形を描いたものです。図のアの部分とイの部分の面積の差を求めなさい。ただし，円周率は3.14とします。
近隣に大手塾が無い！！でも大丈夫。【東進オンライン学校 小学部・中学部】
4.06
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 ＜オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます！しかも授業料は【格安】＞
解答
- 解答を開く
-
下の図は，1辺8cmの正方形ABCDに点Bと点Cを中心とし正方形の1辺を半径として2個のおうぎ形を描いたものです。図のアの部分とイの部分の面積の差を求めなさい。ただし，円周率は3.14とします。
正方形の面積（ア＋イ＋ウ＋ウ）＝64cm2
イ＋ウ＝8×8×3.14×$ \displaystyle \frac{1}{4} $＝50.24cm2
求める面積＝イ－ア
＝（イ＋ウ）＋（イ＋ウ）－（ア＋イ＋ウ＋ウ）
＝50.24×2－64＝36.48cm2（答え） 36.48cm2
ではまた～
