問題
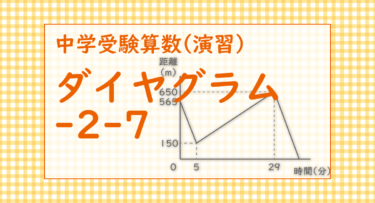
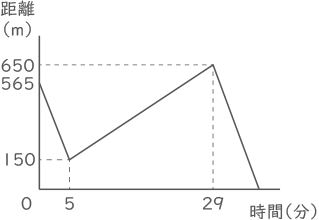太郎村、次郎君、花子さんの3人の家は、学校までのまっすぐな一本道に面しています。太郎君、次郎君、花子さんがこの順にそれぞれの家を出発して、学校までの道をそれぞれ一定の速さで歩き、学校に行きました。右のグラフは、太郎君が家を出発してからの時間と、太郎君と次郎君の間の距離の関係を表したものです。次の［ ］に適当な数を入れなさい。
（1） 次郎君が歩く速さは分速［ア］mで、次郎君の家から学校までの距離は［イ］mです。
（［ア］は帯分数表記で、［イ］は整数表記で答える）
（2） 太郎君が家を出発してから7分後に花子さんは家を出発し、その5分後に花子さんは次郎君に追い越されました。それからさらに10分後に、花子さんは太郎君に追い越されました。花子さんが歩く速さは分速［ウ］mで、花子さんの家から学校までの距離は［エ］mです。
（［ウ］は帯分数表記で、［エ］は小数点入り表記で答える）
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
太郎村、次郎君、花子さんの3人の家は、学校までのまっすぐな一本道に面しています。太郎君、次郎君、花子さんがこの順にそれぞれの家を出発して、学校までの道をそれぞれ一定の速さで歩き、学校に行きました。右のグラフは、太郎君が家を出発してからの時間と、太郎君と次郎君の間の距離の関係を表したものです。次の［ ］に適当な数を入れなさい。（1） 次郎君が歩く速さは分速［ア］mで、次郎君の家から学校までの距離は［イ］mです。
（［ア］は帯分数表記で、［イ］は整数表記で答える）（2） 太郎君が家を出発してから7分後に花子さんは家を出発し、その5分後に花子さんは次郎君に追い越されました。それからさらに10分後に、花子さんは太郎君に追い越されました。花子さんが歩く速さは分速［ウ］mで、花子さんの家から学校までの距離は［エ］mです。
（［ウ］は帯分数表記で、［エ］は小数点入り表記で答える）グラフよりわかること。
・太郎から５分遅れて次郎が歩き出した。
・5分以降太郎と次郎の距離が離れていく。 ⇒ 次郎の進む向きは太郎と同じで、太郎より速く歩く。
・太郎の家は次郎の家より学校に遠く、２人の家の距離は565m。
・次郎は家から学校まで29－5＝24分かかる。
・太郎は5分間に565－150＝415m歩く。
・太郎と次郎が24分間歩くと650－150＝500mの差がつく。（1）
太郎の速さは（565－150）÷5＝83、分速83m
（次郎の速さ－83）×24＝650－150より、次郎の速さは分速103$ \displaystyle \frac{5}{6} $m・・・［ア］次郎の家から学校までの距離は103$ \displaystyle \frac{5}{6} $×（29－5）＝2492ｍ・・・［イ］
（答え） ［ア］103$ \displaystyle \frac{5}{6} $ ［イ］2492
（2）
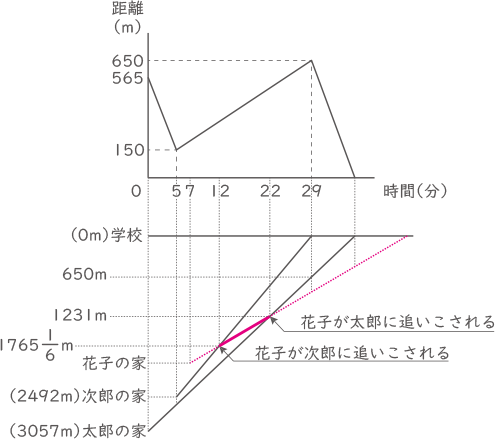
図の様に、3人の学校からの距離と時間をグラフにする。
「12分の点線と次郎の実線の交点」と「22分の点線と太郎の実線の交点」を太い赤線で結ぶと花子の動きが分かる。
太い赤線を延長した赤い点線上に、花子の家の位置と学校までにかかった時間がある。
太郎の家から学校までの距離は2492＋565＝3057m
花子が太郎に追いこされる場所と学校との距離は、
83×22＝1826、3057－1826＝1231m
花子が次郎に追いこされる場所と学校との距離は、
103$ \displaystyle \frac{5}{6} $×（12－5）＝726$ \displaystyle \frac{5}{6} $、2492－726$ \displaystyle \frac{5}{6} $＝1765$ \displaystyle \frac{1}{6} $m花子の歩く速さは、（1765$ \displaystyle \frac{1}{6} $－1231）÷（22－12）より、分速53$ \displaystyle \frac{5}{12} $m・・・［ウ］
花子が5分間に歩く距離は53$ \displaystyle \frac{5}{12} $×5＝267$ \displaystyle \frac{1}{12} $m花子の家から学校までの距離は267$ \displaystyle \frac{1}{12} $＋1765$ \displaystyle \frac{1}{6} $＝2032.25m・・・［エ］
（答え） ［ウ］53$ \displaystyle \frac{5}{12} $ ［エ］2032.25
