問題
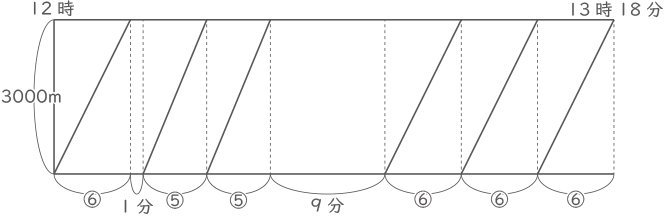
A君は1周3000mの池のまわりを、12時にスタート地点から一定の速さで走り出しました。A君は1周走ったあと、スタート地点で1分休んでから1周目の速さの1.2倍の速さで2周し、さらにスタート地点で9分休んでから1周目の速さにもどして3周すると、合計で6周走り、走り終えた時刻は13時18分でした。
(1) A君が1周目の速さの1.2倍の速さで2周走るときにかかった時間は、A君がスタートしてから1周走るときにかかった時間の何倍ですか。分数で答えなさい。
(2) 1周目のA君の走る速さは分速何mですか。
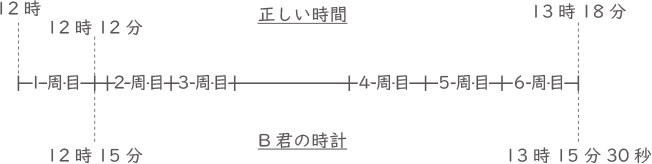
B君の時計は正しくない一定の速さで進みます。A君が1周目を走り終えたとき、B君の時計は12時15分でした。
また、A君が6周目を走り終えたとき、B君の時計は13時15分30秒でした。
(3) B君の時計は正しい時間の何倍の速さで進みますか。分数で答えなさい。
(4) B君の時計が正しい時刻を示したとき、その時刻を答えなさい。またそのとき、A君はスタートしてから全部で何km走りましたか。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
A君は1周3000mの池のまわりを、12時にスタート地点から一定の速さで走り出しました。A君は1周走ったあと、スタート地点で1分休んでから1周目の速さの1.2倍の速さで2周し、さらにスタート地点で9分休んでから1周目の速さにもどして3周すると、合計で6周走り、走り終えた時刻は13時18分でした。
(1) A君が1周目の速さの1.2倍の速さで2周走るときにかかった時間は、A君がスタートしてから1周走るときにかかった時間の何倍ですか。分数で答えなさい。
(2) 1周目のA君の走る速さは分速何mですか。
B君の時計は正しくない一定の速さで進みます。A君が1周目を走り終えたとき、B君の時計は12時15分でした。
また、A君が6周目を走り終えたとき、B君の時計は13時15分30秒でした。(3) B君の時計は正しい時間の何倍の速さで進みますか。分数で答えなさい。
(4) B君の時計が正しい時刻を示したとき、その時刻を答えなさい。またそのとき、A君はスタートしてから全部で何km走りましたか。
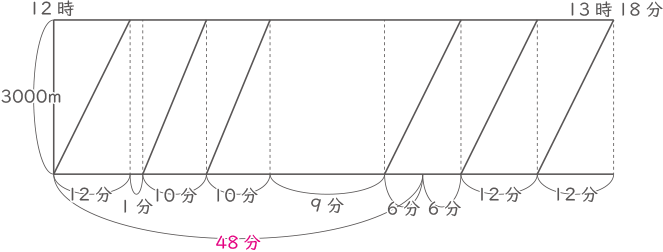
(1)
速さの比が1:1.2=5:6のとき、かかる時間の比は逆比となり⑥:⑤。
これをもとにダイヤグラムをつくる。
$ \displaystyle \frac{⑩}{⑥} $=1$ \displaystyle \frac{2}{3} $倍
(答え) 1$ \displaystyle \frac{2}{3} $倍
(2)
⑥×4+⑤×2+1+9=78より①=2分、⑥=12分
よって、A君の走る速さは3000÷12=250、分速250m。(答え) 分速250m
(3)
A君が1周目を走り終えたのは、(2)より12時12分。
12時12分から13時18分まで66分。
12時15分から13時15分30秒まで60分30秒。
$ \displaystyle \frac{60.5}{66} $=$ \displaystyle \frac{11}{12} $
(答え) $ \displaystyle \frac{11}{12} $倍
(4)
正しい時間が1秒進むとB君の時計は$ \displaystyle \frac{11}{12} $秒進むので、1秒あたり正しい時計より$ \displaystyle \frac{1}{12} $秒遅れる。
180秒遅れるのは、
$ \displaystyle \frac{1}{12} $×□=180より、□=2160となり36分後の12時48分。
3000×3.5=10500より10.5km
(答え) 12時48分で10.5km