問題
太郎はA地点を出発しB地点へ、学は太郎より10分遅(おく)れてB地点を出発しA地点へそれぞれ歩いて向かいました。太郎の歩く速さは毎分60mで、出発してから42分後に学と出会いました。そこで太郎は忘れ物に気づいたので、走ってA地点に戻り、すぐに走ってB地点に向かいました。学は太郎と出会った地点で5分休み、再びA地点へ向かいました。太郎がB地点に着いた時刻と、学がA地点に着いた時刻は同じでした。
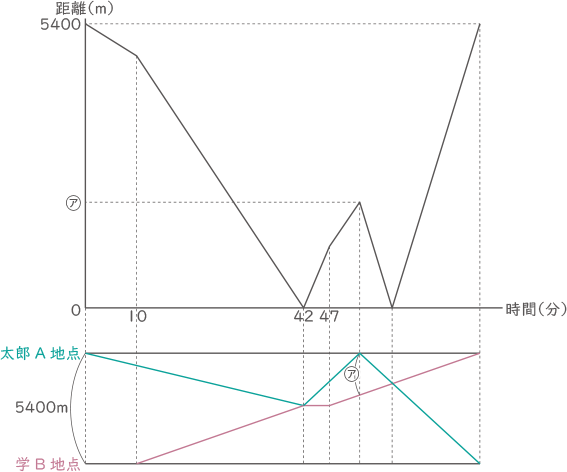
下の図は、太郎が最初にA地点を出発してからの時間と太郎と学の間の距離(きょり)の関係を表したものです。
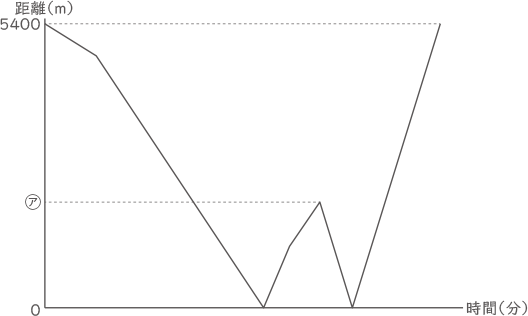
このとき、次の問いに答えなさい。ただし、学の歩く速さと太郎の走る速さはそれぞれ一定であるとします。
(1) 学の歩く速さを求めなさい。
(2) 太郎の走る速さを求めなさい。
(3) ㋐に当てはまる数を求めなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
太郎はA地点を出発しB地点へ、学は太郎より10分遅(おく)れてB地点を出発しA地点へそれぞれ歩いて向かいました。太郎の歩く速さは毎分60mで、出発してから42分後に学と出会いました。そこで太郎は忘れ物に気づいたので、走ってA地点に戻り、すぐに走ってB地点に向かいました。学は太郎と出会った地点で5分休み、再びA地点へ向かいました。太郎がB地点に着いた時刻と、学がA地点に着いた時刻は同じでした。
下の図は、太郎が最初にA地点を出発してからの時間と太郎と学の間の距離(きょり)の関係を表したものです。
このとき、次の問いに答えなさい。ただし、学の歩く速さと太郎の走る速さはそれぞれ一定であるとします。
(1) 学の歩く速さを求めなさい。
(2) 太郎の走る速さを求めなさい。
(3) ㋐に当てはまる数を求めなさい。
(1)
太郎が出発して10分経ったときの2人の距離は5400-60×10=4800m。
学が出発してから32分で2人は出会うので、学の歩く速さを毎分□mとすると
4800=(60+□)×32より、□=90、学の歩く速さは毎分90m。(答え) 毎分90m
(2)
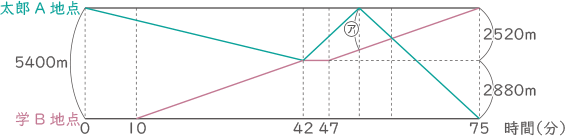
学の5400mを歩く時間は、5400÷90=60より60分、よって、太郎が出発してから75分後に2人は各地点に到着した。
学は出発してから32分で太郎に出会うので、その場所は90×32=2880、B地点から2880m、A地点から2520m。
太郎の走った距離は2520+5400=7920mで、かかった時間は75-42=33分。
よって、太郎の走る速さは7920÷33=240、毎分240m。(答え) 毎分240m
(3)
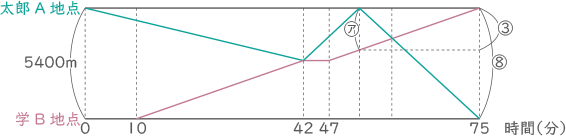
太郎の走る速さ:学の歩る速さ=240:90=⑧:③
⑧が5400mであれば③は5400×$ \displaystyle \frac{3}{8} $=2025、㋐は2025mとなる。
(答え) 2025