問題
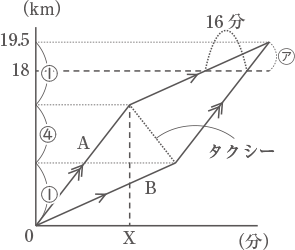
A とBが同時に会社を出発して18km離れたO会社へ向かいます。Aは初めタクシーに乗り，途中で降りて徒歩で向かいました。Bは初め徒歩で向かいましたが，Aを乗せていたタクシーが戻ってきたのでそれに乗ってO会社に向かったところ，Aより16分遅れて到着しました。タクシーの走る速さは毎時45km，2人の歩く速さは毎時5kmです。グラフはかかった時間と距離の関係を表したものです。
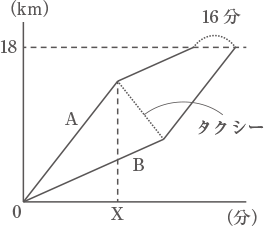（1） 2人が同時に到着するためには，Aは出発して何kmのところでタクシーを降りればよいですか。
（2） グラフのXはいくつですか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ！ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
A とBが同時に会社を出発して18km離れたO会社へ向かいます。Aは初めタクシーに乗り，途中で降りて徒歩で向かいました。Bは初め徒歩で向かいましたが，Aを乗せていたタクシーが戻ってきたのでそれに乗ってO会社に向かったところ，Aより16分遅れて到着しました。タクシーの走る速さは毎時45km，2人の歩く速さは毎時5kmです。グラフはかかった時間と距離の関係を表したものです。
（1） 2人が同時に到着するためには，Aは出発して何kmのところでタクシーを降りればよいですか。
（2） グラフのXはいくつですか。【類似問題：ダイヤグラム2-2（車を使ったピストン輸送＋徒歩）】
（1）
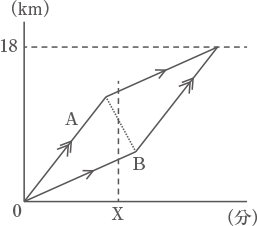
2人が同時に到着するときのグラフは図の様な平行四辺形となる。
タクシーの走る速さは毎時45km、2人の歩く速さは毎時5km、よって、同じ時間に進む距離は、タクシー：B＝45：5＝⑨：①となる。同様に、タクシー：A＝45：5＝9⃣：1⃣となる。
これを距離の比で見ると図の様になる。
よって、Aの降りるところは
18×$ \displaystyle \frac{⑤}{⑥} $＝15、Aは出発して15kmのところでタクシーを降りればよい。（答え） 15kmのところ
（2）
18kmから先に線を延長して（1）のように平行四辺形をつくる。
タクシーの速さは時速45km＝分速750m・・・（ⅰ）
A，Bの速さは時速5km＝分速$ \displaystyle \frac{250}{3} $m・・・（ⅱ）
図の㋐の距離は、Bが徒歩でかかる時間とタクシーでかかる時間の差である16分から求められる。
（□÷$ \displaystyle \frac{250}{3} $－□÷750＝16からでも求められるが今回は16分という分かりやすい数字が用意されている。）
（ⅰ）と（ⅱ）をいくつか計算して比べると、
B：18分で1500m
タクシー：2分で1500m
が見つかる。16分の差は1500m（㋐）とわかる。
さらに、（1）と同様にたてじくに①：④：①の比をわりあてる。
グラフのXは、
19.5×$ \displaystyle \frac{⑤}{⑥} $÷45=$ \displaystyle \frac{13}{36} $時間、単位を分に直す。$ \displaystyle \frac{13}{36} $×60＝$ \displaystyle \frac{65}{3} $＝21$ \displaystyle \frac{2}{3} $分
（答え） 21$ \displaystyle \frac{2}{3} $
2人が同時に到着するときのグラフは図の様な平行四辺形となる。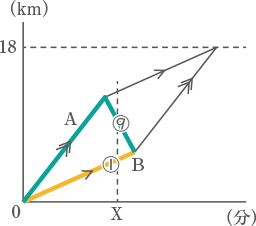
タクシーの走る速さは毎時45km、2人の歩く速さは毎時5km、よって、同じ時間に進む距離は、タクシー：B＝45：5＝⑨：①となる。
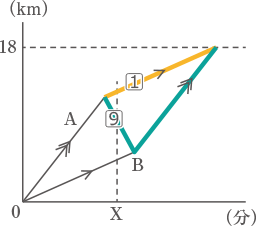同様に、タクシー：A＝45：5＝9⃣：1⃣となる。
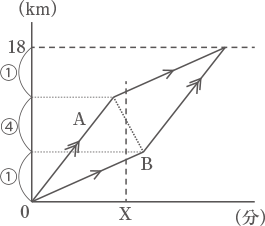これを距離の比で見ると図の様になる。
