問題
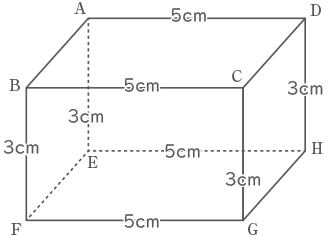
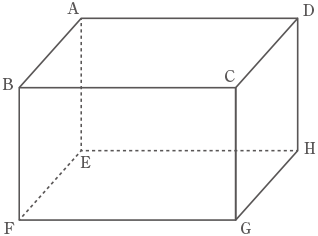
図のような,面ABCDと面BFEAの面積の比が5:3で, 辺BCの長さが5cmの直方体があります。
次の間いに答えなさい。
(1) 直方体のすべての辺の長さの和が48cmであるとき,この直方体の体積を求めなさい。
(2) 直方体の表面積が70cm2であるとき,この直方体の体積を求めなさい。
(3) 直方体の体積が90cm3であるとき,この直方体の表面積を求めなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
図のような,面ABCDと面BFEAの面積の比が5:3で, 辺BCの長さが5cmの直方体があります。
次の間いに答えなさい。
(1) 直方体のすべての辺の長さの和が48cmであるとき,この直方体の体積を求めなさい。
(2) 直方体の表面積が70cm2であるとき,この直方体の体積を求めなさい。
(3) 直方体の体積が90cm3であるとき,この直方体の表面積を求めなさい。
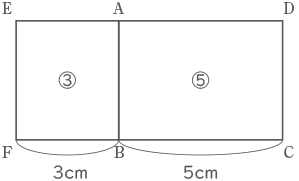
四角形ABFEと四角形ABCDを展開図で見ると、面積が③:⑤で高さABが共通なので辺BFは3cmとわかる。

これで、分からない長さは辺ABと同じ長さのところだけ。
(1)
辺ABの長さ=(48-5×4-3×4)÷4=4cm
直方体の体積=5×3×4=60cm3(答え) 60cm3
(2)
四角形BCGFと四角形ADHEの面積は合わせて3×5×2=30cm2であり、残りの4面の面積は70-30=40cm2となるので、辺ABの長さは40÷(5+3+5+3)=2.5cmとなる。
直方体の体積=5×3×2.5=37.5cm3(答え) 37.5cm3
(3)
辺ABの長さ×3×5=90cm3なので、辺ABの長さは6cm、
直方体の表面積=(5×3+5×6+3×6)×2=126cm2(答え) 126cm2