場合の数-2-3（海城中学2022/この手の問題を苦手とする子は多い）

問題

解答

 解答を開く

 

777枚のコインは片方の面が白色，もう片方の面が黒色であり，1～777の番号がついています。はじめ，コインは全て白色の面が上になっています。また，袋（ふくろ）の中に1～5の数字が書かれたカードが1枚ずつ計5枚あり，次の【操作】をくり返し行います。

【操作】
カードを1枚引き，引いたカードの数字の倍数の番号のコインを裏返す。
その後，引いたカードを袋の中にもどす。

例えば，【操作】を2回行い，引いたカードの数字が順に2，3であったとき，2，3，4の番号のコインは黒色の面が上になっていますが，6の番号のコインは白色の面が上になっています。次の問いに答えなさい。

（1） 【操作】を2回行い，引いたカードの数字が順に2，4であったとき，黒色の面が上になっているコインは何枚ですか。
（2） 【操作】を3回行い，引いたカードの数字が順に2，3，1であったとき，黒色の面が上になっているコインは何枚ですか。
（3） 【操作】を11回行ったとき，どのようなカードの引き方をしても必ず黒色の面が上になっているコインは何枚ですか。

 

---

 

（1）
引いたカードが２のとき、その倍数で裏返すのは388枚のコイン（777÷2＝388あまり1）。
次に引いたカードが4のとき、その倍数で裏返すのは194枚のコイン（777÷4＝194あまり1）。この194枚のコインは1つ前の【操作】で全て裏返ったもの。
よって、黒色の面が上になっているコインは388－194=194枚。

（答え）　194枚

 

（2）
引いたカードが２のとき、その倍数で裏返すのは388枚のコイン（777÷2＝388あまり1）。
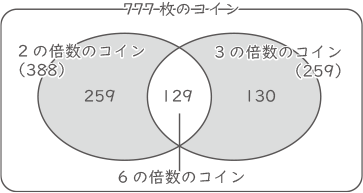
引いたカードが3のとき、その倍数で裏返すのは259枚のコイン（777÷3＝259あまり0）。
2と3の最小公倍数6の倍数のコインは再び表になり、その枚数は129（777÷6＝129あまり3）。
この時点で黒色の面が上になっているコインは（388－129）＋（259－129）＝389枚。

引いたカードが1のとき、その倍数で裏返すのは全コイン。
よって、黒色の面が上になっているコインは777－389＝388枚。

（答え）　388枚

 

（3）
11回の操作で毎回裏返すのであれば、11回目は黒の面が上になる。
【どのようなカードの引き方をしても必ず黒色の面が上になる】ためには、毎回1～5のどの数字を引いても必ず裏返しになれはよい。
↓
1～5の最小公倍数の倍数であればよい。
1～5の最小公倍数は60なので、777÷60＝12あまり57
よって、12枚。

（答え）　12枚