問題
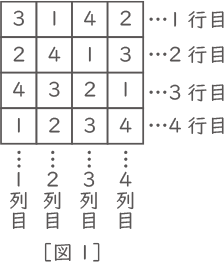 縦4個、横4個の合計16個のマス目のそれぞれに、1、2、3、4いずれかの数字を入れていきます。このマス目の横の並びを行といい、縦の並びを列といいます。どの行にも、どの列にも同じ数字が1回しか現れない入れ方が何通りあるかについて考えます。
縦4個、横4個の合計16個のマス目のそれぞれに、1、2、3、4いずれかの数字を入れていきます。このマス目の横の並びを行といい、縦の並びを列といいます。どの行にも、どの列にも同じ数字が1回しか現れない入れ方が何通りあるかについて考えます。
[図1]はこの入れ方に従って数字を入れた一例です。
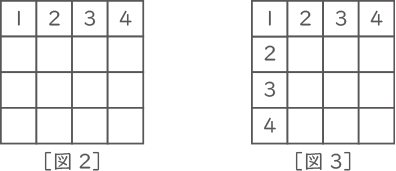
まず、[図2] のように、1行目に左から1、2、3、4の順に数字が入っている場合について考えます。
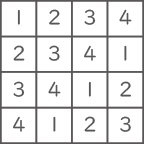
続いて1列目の残りの3つのマス目に、[図3] のように、上から順に2、3、4と数字を入れます。
 (1)
(1)
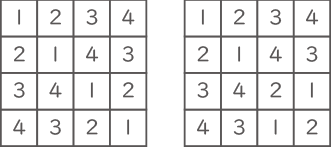
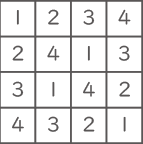
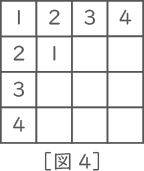
[図4]のように2行2列日に1を入れたとき、残り8マスの数字の入れ方は2通りあります。この2通りの数字の入れ方を解答用紙の2つの図のマス目に書き入れなさい。
以下、<ア>~<キ>にあてはまる数をそれぞれ求めなさい。
(2)
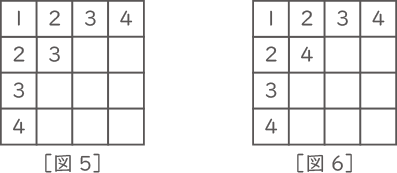
[図5]のように2行2列日に3を入れたとき、残り8マスの数字の入れ方は[ ア ]通り、[図6]のように2行2列目に4を入れたとき、残り8マスの数字の入れ方は[ イ ]通りあります。このことと(1)の結果を用いて、[図3]の状態の残り9マスの数字の入れ方は全部で[ ウ ]通りあるとわかります。
(3)
(2)のようにして16マスすべて埋(う)まった数字の並びのそれぞれについて、1行目は動かさずに、2~4行目だけを行ごと入れ替(か)えることで、異なる数字の並びを作ることができます。
2、3、4の3つの数字を一列に並べる並べ方は[ エ ]通りあるので、これらのことと(2)の結果を用いて、[図2]の状態の残り12マスの数字の入れ方は全部で[ オ ]通りあるとわかります。
(4)
すべてのマス目が空白の状態のとき、1行目の4つのマス目に1、2、3、4の数字を同じ数字が1回しか現れないように入れる入れ方は全部で[ カ ]通りあります。このことと(3)の結果を用いて、この16個のマス目の数字の入れ方は全部で[ キ ]通りあるとわかります。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
 縦4個、横4個の合計16個のマス目のそれぞれに、1、2、3、4いずれかの数字を入れていきます。このマス目の横の並びを行といい、縦の並びを列といいます。どの行にも、どの列にも同じ数字が1回しか現れない入れ方が何通りあるかについて考えます。
縦4個、横4個の合計16個のマス目のそれぞれに、1、2、3、4いずれかの数字を入れていきます。このマス目の横の並びを行といい、縦の並びを列といいます。どの行にも、どの列にも同じ数字が1回しか現れない入れ方が何通りあるかについて考えます。
[図1]はこの入れ方に従って数字を入れた一例です。まず、[図2] のように、1行目に左から1、2、3、4の順に数字が入っている場合について考えます。
続いて1列目の残りの3つのマス目に、[図3] のように、上から順に2、3、4と数字を入れます。
 (1)
(1)
[図4]のように2行2列日に1を入れたとき、残り8マスの数字の入れ方は2通りあります。この2通りの数字の入れ方を解答用紙の2つの図のマス目に書き入れなさい。以下、<ア>~<キ>にあてはまる数をそれぞれ求めなさい。
(2)
[図5]のように2行2列日に3を入れたとき、残り8マスの数字の入れ方は[ ア ]通り、[図6]のように2行2列目に4を入れたとき、残り8マスの数字の入れ方は[ イ ]通りあります。このことと(1)の結果を用いて、[図3]の状態の残り9マスの数字の入れ方は全部で[ ウ ]通りあるとわかります。
(3)
(2)のようにして16マスすべて埋(う)まった数字の並びのそれぞれについて、1行目は動かさずに、2~4行目だけを行ごと入れ替(か)えることで、異なる数字の並びを作ることができます。
2、3、4の3つの数字を一列に並べる並べ方は[ エ ]通りあるので、これらのことと(2)の結果を用いて、[図2]の状態の残り12マスの数字の入れ方は全部で[ オ ]通りあるとわかります。(4)
すべてのマス目が空白の状態のとき、1行目の4つのマス目に1、2、3、4の数字を同じ数字が1回しか現れないように入れる入れ方は全部で[ カ ]通りあります。このことと(3)の結果を用いて、この16個のマス目の数字の入れ方は全部で[ キ ]通りあるとわかります。(1)
(答え)

(2)-ア
1通りだけ
(答え) 1
(2)-イ
1通りだけ
(答え) 1
(2)-ウ
2通り+1通り+1通り=4通り(答え) 4
(3)-エ
2、3、4の並べ方は3×2×1=6通り(答え) 6
(3)-オ
4通り×6通り=24通り(答え) 24
(4)-カ
1、2、3、4の並び順は4×3×2×1=24通り(答え) 24
(4)-キ
24通り×24通り=576通り(答え) 576