問題
各位の数の和が各位の数の積以上である3桁の整数A を考えます。たとえば,925の各位の数の和は9+2+5=16,各位の数の積は9×2×5=90となり,925は整数Aとしてふさわしくありません。
このとき,次の問いに答えなさい。
(1)百の位の数が9である整数Aは全部で何個ありますか。
(2)3つの位の数の中に0を含む整数Aは全部で何個ありますか。
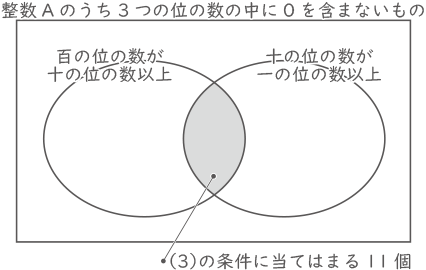
(3)次の3つの条件すべてにあてはまる整数Aは全部で何個ありますか。
・3つの位の数の中に0はない。
・百の位の数は十の位の数以上である。
・十の位の数は一の位の数以上である。
(4)整数Aは全部で何個ありますか。
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 <オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます!しかも授業料は【格安】>
解答
- 解答を開く
-
各位の数の和が各位の数の積以上である3桁の整数A を考えます。たとえば,925の各位の数の和は9+2+5=16,各位の数の積は9×2×5=90となり,925は整数Aとしてふさわしくありません。
このとき,次の問いに答えなさい。(1)百の位の数が9である整数Aは全部で何個ありますか。
(2)3つの位の数の中に0を含む整数Aは全部で何個ありますか。
(3)次の3つの条件すべてにあてはまる整数Aは全部で何個ありますか。
・3つの位の数の中に0はない。
・百の位の数は十の位の数以上である。
・十の位の数は一の位の数以上である。(4)整数Aは全部で何個ありますか。
(1)
(十の位と一の位に0があれば各位の数の積は全て0になる)
十の位の数が0の場合、一の位は0~9の10個。
一の位の数が0の場合、十の位は0~9の10個。ただし、900は上で数えているので1個引いて9個。
十の位も一の位も0でないときは911の1個。
合わせて10+9+1=20個。(答え) 20個
(2)
百の位は1~9のどれかとなる。
十の位の数が0の場合、一の位は0~9の10個。
一の位の数が0の場合、十の位は0~9の10個。ただし、下二桁が00の数は上で数えているので1個引いて9個。
よって、9×(10+9)=171個。(答え) 171個
(3)
百の位が1の場合
111の1個。百の位が2の場合
221・211の2個。百の位が3の場合
321・311の2個。百の位が4の場合
411の1個。百の位が5の場合
511の1個。百の位が6の場合
611の1個。百の位が7の場合
711の1個。百の位が8の場合
811の1個。百の位が9の場合
911の1個。計、1+2+2+1+1+1+1+1+1=11個
(答え) 11個
(4)
0を含む整数Aは(2)で全て数えてある。(171個)
0を含まない整数Aについては下図のとおり。
0を含まない整数Aのうち数えていないものは、【百の位の数が十の位の数より小さいもの】または【十の位の数が一の位の数より小さいもの】なので、これについて数える。
【百の位の数が十の位の数より小さいもの】
百の位が1の場合
121・122・123・131・132・141・151・161・171・181・191百の位が2の場合
231百の位が3の場合、百の位が4の場合、百の位が5の場合、百の位が6の場合、百の位が7の場合、百の位が8の場合、百の位が9の場合
なし【十の位の数が一の位の数より小さいもの】
十の位が1の場合
112・212・312・113・213・114・115・116・117・118・119十の位が2の場合
123十の位が3の場合、十の位が4の場合、十の位が5の場合、十の位が6の場合、十の位が7の場合、十の位が8の場合、十の位が9の場合
なし計24個で重複している123を除くと23個
全て加算すると171+11+23=205個
(答え) 205個