問題
（原文ママとするため図6～8とする）
図6のような，縦4マス，横4マスのマス目があります。このマス目の中を，次の規則にしたがって，整数を書きこみながら移動します。
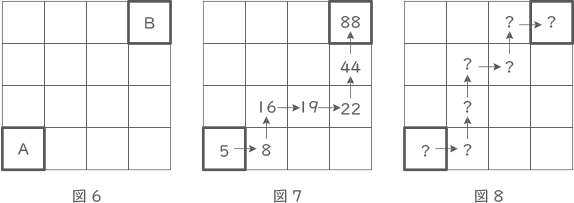
規則
・左下のAのマスに整数を書きこみます。
・左下のAのマスから移動を開始し，右上のBのマスまで移動します。
・右または上に1マスずつ移動します。
・右に移動するときは，移動する前のマスに書かれた数に3を加えた数を記入します。上に移動するときは，移動する前のマスに書かれた数を2倍した数を記入します。
例えば，図7のように移動するとき，Aのマスの数が5であれば，Bのマスの数は88になります。
（1） 図8のような経路で移動するときを考えます。
① Aのマスの数が7のとき，Bのマスの数を求めなさい。
② Bのマスの数が2桁の整数になるとき，Bのマスの数として考えられる整数のうち，最大の数を求めなさい。
（2） Bのマスの数が2022であるとき，Aのマスの数として考えられる整数をすべて答えなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
（原文ママとするため図6～8とする）
図6のような，縦4マス，横4マスのマス目があります。このマス目の中を，次の規則にしたがって，整数を書きこみながら移動します。
規則
・左下のAのマスに整数を書きこみます。
・左下のAのマスから移動を開始し，右上のBのマスまで移動します。
・右または上に1マスずつ移動します。
・右に移動するときは，移動する前のマスに書かれた数に3を加えた数を記入します。上に移動するときは，移動する前のマスに書かれた数を2倍した数を記入します。例えば，図7のように移動するとき，Aのマスの数が5であれば，Bのマスの数は88になります。
（1） 図8のような経路で移動するときを考えます。
① Aのマスの数が7のとき，Bのマスの数を求めなさい。
② Bのマスの数が2桁の整数になるとき，Bのマスの数として考えられる整数のうち，最大の数を求めなさい。（2） Bのマスの数が2022であるとき，Aのマスの数として考えられる整数をすべて答えなさい。
（1）
7→10↑20↑40→43↑86→89（答え） 89
（2）
① Bに入りうる最大値は99
② 1つ前のマスは96
③ 2つ前のマスは48
④ 3つ前のマスは45
⑤ 4つ前のマスは22.5、しかし整数なので22
⑥ 5つ前のマスは11
⑦ 6つ前のマスは8⑤のことより、22↑44→47↑94→97
（答え） 97
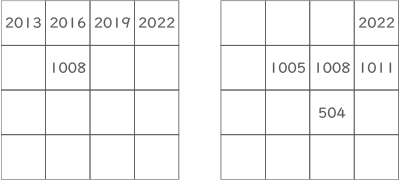
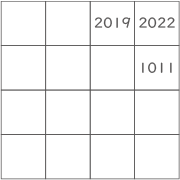
（3）
2022の1つ前のマスは2019か1011。
2019の1つ前のマスは2016のみ。
1011の1つ前のマスは1008のみ。2016の1つ前のマスは2013か1008。
1008の1つ前のマスは1005か504。
2013の1つ前のマスはなし。
1008の1つ前のマスは1005か504。
1005の1つ前のマスは1002。
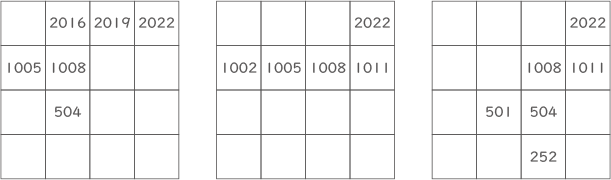
504の1つ前のマスは501か252。
1005の1つ前のマスはなし。
504の1つ前のマスは501か252。
1002の1つ前のマスは501。
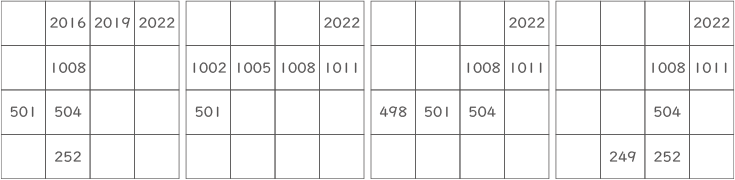
501の1つ前のマスは498。
252の1つ前のマスは249。
501の1つ前のマスはなし。
252の1つ前のマスは249。
501の1つ前のマスはなし。
498の1つ前のマスは249。
249の1つ前のマスは246。（答え） 246と249
2022の1つ前のマスは2019か1011。
