問題
大小2つの正三角形があります。大きい正三角形ACEの各辺の真ん中に小さい正三角形BDFの頂点があり、頂点Bは辺ACの真ん中に、頂点Dは辺CEの真ん中に、頂点Fは辺EAの真ん中にあります。
この2つの正三角形の辺上を動く点をP、Qとし、点Pは正三角形ACEの辺上を頂点Aから、点Qは正三角形BDFの辺上を頂点Dから、反時計回りに同時に動き始め、点Qは1秒間に1辺分動き、点Pは点Qと同じ速さで動きます。
点P、Qを直線で結び、できあがった直線の真ん中の点をMとします。正三角形ACEの面積を16として、点P、Qが動き始めてから5秒間で点Mによってつくられる図形の面積を求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
大小2つの正三角形があります。大きい正三角形ACEの各辺の真ん中に小さい正三角形BDFの頂点があり、頂点Bは辺ACの真ん中に、頂点Dは辺CEの真ん中に、頂点Fは辺EAの真ん中にあります。
この2つの正三角形の辺上を動く点をP、Qとし、点Pは正三角形ACEの辺上を頂点Aから、点Qは正三角形BDFの辺上を頂点Dから、反時計回りに同時に動き始め、点Qは1秒間に1辺分動き、点Pは点Qと同じ速さで動きます。
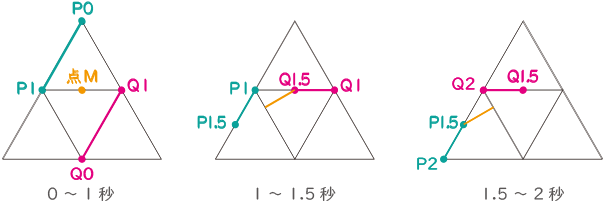
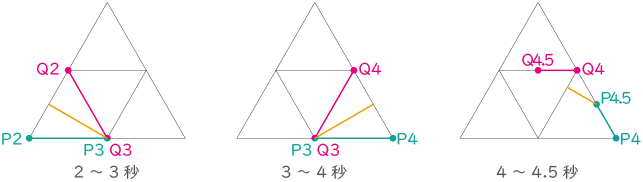
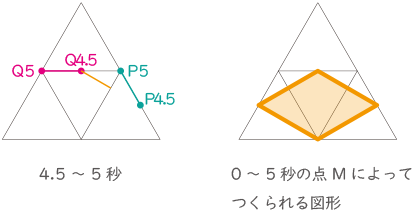
点P、Qを直線で結び、できあがった直線の真ん中の点をMとします。正三角形ACEの面積を16として、点P、Qが動き始めてから5秒間で点Mによってつくられる図形の面積を求めなさい。
図の様な2つの正三角形があり、点P、Qがそれぞれの正三角形の辺上を動く。その点P、Qを直線で結び、できあがった直線の真ん中の点Mの動きを時間の経過毎に記入していく。
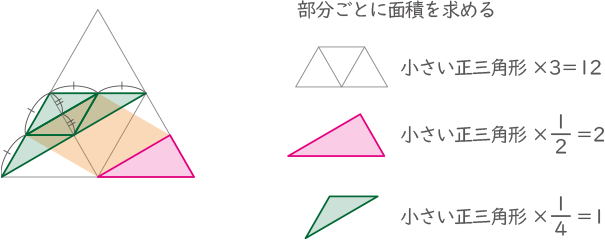
よって、12－2×2－1×2＝6
（答え）6
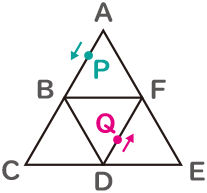図の様な2つの正三角形があり、点P、Qがそれぞれの正三角形の辺上を動く。その点P、Qを直線で結び、できあがった直線の真ん中の点Mの動きを時間の経過毎に記入していく。
