問題
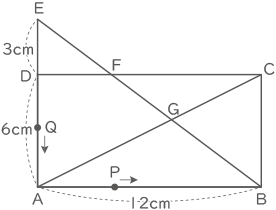 周囲の長さが等しい長方形ABCD と直角三角形ABEが図のように重なっていて、さらに長方形の対角線ACを引きます。辺CDと辺BEの交点をF、対角線ACと辺BEの交点をGとします。
周囲の長さが等しい長方形ABCD と直角三角形ABEが図のように重なっていて、さらに長方形の対角線ACを引きます。辺CDと辺BEの交点をF、対角線ACと辺BEの交点をGとします。
点Pは秒速2cmで長方形の辺上を点Aから出発して反時計回り(点Bの方へ)に動きます。点Qは秒速3cmで直角三角形の辺上を点Eから出発して反時計回り(点Aの方へ)に動いて1周します。点Pと点Qは同時に動き始めます。このとき、次の問いに答えなさい。
(1) 点Qが1周するのにかかる時間は何秒ですか。
(2) BGの長さは何cmですか。
(3) 点Qが1周するまでの間で、3点A、P、Qをそれぞれ結んだとき三角形ができないのは、動き始めて[①]秒後から[②]秒後までの間と、動き始めて[③]秒後です。
[①]~[③]にあてはまる数は何ですか。
(4) 動き始めて8秒後の三角形APQの面積は何cm2ですか。途中の考え方や式も書きなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
 周囲の長さが等しい長方形ABCD と直角三角形ABEが図のように重なっていて、さらに長方形の対角線ACを引きます。辺CDと辺BEの交点をF、対角線ACと辺BEの交点をGとします。
周囲の長さが等しい長方形ABCD と直角三角形ABEが図のように重なっていて、さらに長方形の対角線ACを引きます。辺CDと辺BEの交点をF、対角線ACと辺BEの交点をGとします。
点Pは秒速2cmで長方形の辺上を点Aから出発して反時計回り(点Bの方へ)に動きます。点Qは秒速3cmで直角三角形の辺上を点Eから出発して反時計回り(点Aの方へ)に動いて1周します。点Pと点Qは同時に動き始めます。このとき、次の問いに答えなさい。(1) 点Qが1周するのにかかる時間は何秒ですか。
(2) BGの長さは何cmですか。
(3) 点Qが1周するまでの間で、3点A、P、Qをそれぞれ結んだとき三角形ができないのは、動き始めて[①]秒後から[②]秒後までの間と、動き始めて[③]秒後です。
[①]~[③]にあてはまる数は何ですか。
(4) 動き始めて8秒後の三角形APQの面積は何cm2ですか。途中の考え方や式も書きなさい。(1)
直角三角形ABEの周囲の長さは(6+12)×2=36cmなので、36÷3=12秒。(答え) 12秒
(2)
三角形AGEと三角形CGBは相似なのでAE:CB=9:6=GE:GB=3:2となる。また、BE=36-(3+6+12)=15cmより、BG=15×$ \displaystyle \frac{2}{5} $=6cmとなる。(答え) 6cm
(3)
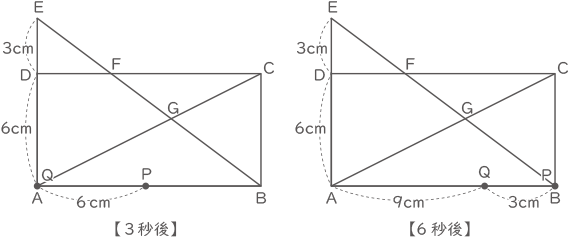
【3秒後】
点QはEから9cm進んだところ(A)で、
点PはAから6cm進んだところ、よって、3点は一直線となる。
【6秒後】
点PはAから12cm進んだところ(B)で、
点QはEから18cm進んだところ、よって、3点は一直線となる。
3秒後から6秒後まで一直線となり三角形が出来ない。
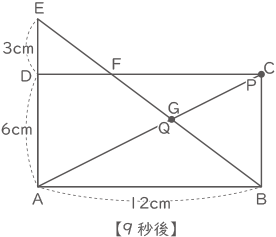
 【9秒後】
【9秒後】
点PはAから18cm進んだところ(C)で、
点QはEから27cm進んだところ(G)、
よって、3点は一直線となり三角形が出来ない。(答え) ① 3 ② 6 ③ 9
(4)
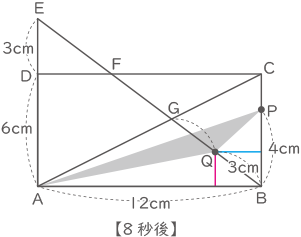
【8秒後】
9秒後より1秒手前なので、
点PはCから2cm戻ったところ。
点QはGから3cm戻ったところ。
図の様に、Qから垂直に伸ばした赤線の長さは、3:15=赤線の長さ:9より1.8cm。
Qから水平に伸ばした青線の長さは、1.8:6=青線の長さ:8(CF)より2.4cm。
求める面積=ABP-ABQ-BPQより、
(12×4÷2)-(12×1.8÷2)-(4×2.4÷2)=8.4cm2
(答え) 8.4cm2


 【9秒後】
【9秒後】