問題
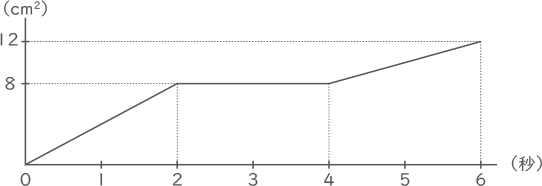
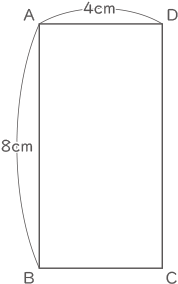AB=8cm、AD=4cmの長方形ABCDがあります。2点E、Fは頂点Bを同時に出発して、この長方形の辺上を頂点Cを通って頂点Dへ向かって動き、点Eが頂点Dに到達した時点で2点E、Fはどちらも止まります。点Eの速さは秒速2cm、点Fの速さは秒速1cmです。長方形ABCDの辺と、AEとAFにはさまれた部分の面積を考えます。このとき、次の問いに答えなさい。
（1） 1秒後の面積を求めなさい。
（2） 3秒後の面積を求めなさい。
（3） 面積が変わらないのは何秒後から何秒後までですか。
（4） 面積が一番大きくなるのは何秒後になりますか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
AB=8cm、AD=4cmの長方形ABCDがあります。2点E、Fは頂点Bを同時に出発して、この長方形の辺上を頂点Cを通って頂点Dへ向かって動き、点Eが頂点Dに到達した時点で2点E、Fはどちらも止まります。点Eの速さは秒速2cm、点Fの速さは秒速1cmです。長方形ABCDの辺と、AEとAFにはさまれた部分の面積を考えます。このとき、次の問いに答えなさい。（1） 1秒後の面積を求めなさい。
（2） 3秒後の面積を求めなさい。
（3） 面積が変わらないのは何秒後から何秒後までですか。
（4） 面積が一番大きくなるのは何秒後になりますか。
（1）
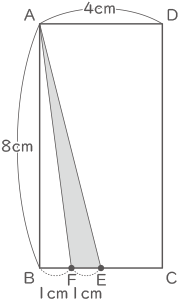
1秒後の2点の位置は図の通り。
1×8÷２＝4cm2（答え） 4cm2
（2）
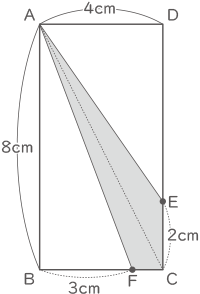
3秒後の2点の位置は図の通り。
（1×8÷2）＋（2×4÷2）＝8cm2（答え） 8cm2
（3）
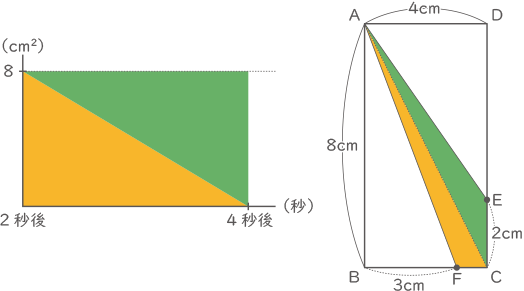
2秒後から4秒後までが分かりづらいので、２つの三角形の面積に分けてグラフに書いてみると、一定の面積になることがわかる。
（答え） 2秒後から4秒後まで
（4）
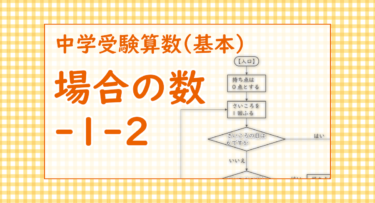
面積は一定の割合で変化していくので全体のグラフを書いてみると6秒後が面積が1番大きくなる。
（答え） 6秒後
（1）
（2）
