問題
問題(正方形と正五角形の辺上を動く点)
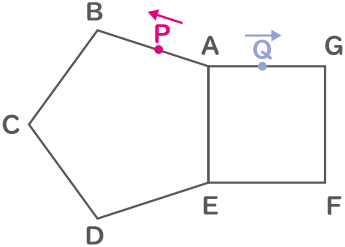
図の様に1辺が10cmの正五角形と正方形があります。点Pは正五角形の辺上を頂点Aから反時計回りに秒速5cmで、点Qは正方形の辺上を頂点Aから時計回りに秒速2cmで同時に動き出します。
(1)点P、Qが初めて頂点Aで出会うのは動き出してから何秒後ですか。
(2)点Pが29回目に頂点Aに戻った時、点Qのいる位置はどこですか。
【家庭学習】過去問をA3で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
図の様に1辺が10cmの正五角形と正方形があります。点Pは正五角形の辺上を頂点Aから反時計回りに秒速5cmで、点Qは正方形の辺上を頂点Aから時計回りに秒速2cmで同時に動き出します。
(1)点P、Qが初めて頂点Aで出会うのは動き出してから何秒後ですか。
(2)点Pが29回目に頂点Aに戻った時、点Qのいる位置はどこですか。

(1)
点Pが頂点Aに戻るのは、10秒後、20秒後、30秒後・・・、点Qが頂点Aに戻るのは、20秒後、40秒後、60秒後・・・であり、共通なのは20秒後。(答え) 20秒後
(2)
点Pは1周10秒かかるので、29周では290秒かかる。290秒でQは2×290=580cm進む。
580÷40=14あまり20なので、点Qは14周と20cm進み、その時の位置は頂点Fとなる。(答え) 頂点F
ではまた~