問題
問題(正方形の辺上を動く2点)
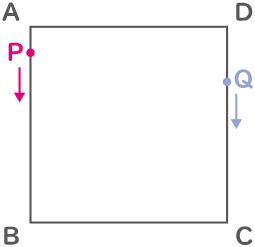
図の様な1辺が48cmの正方形の辺上を、点Pが頂点Aから秒速4cmで反時計回りに、点Qが頂点Dから秒速8cmで時計回りに同時に動き始めます。
(1) 点P、Qが初めて出会うのは何秒後ですか。
(2) 点P、Qが初めて辺ABと平行になるのは何秒後ですか。
(3) 点P、Qが初めて同時にもとの位置に戻るのは何秒後ですか。
関西で一番信頼出来る中学受験塾「浜学園」
4.72
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
図の様な1辺が48cmの正方形の辺上を、点Pが頂点Aから秒速4cmで反時計回りに、点Qが頂点Dから秒速8cmで時計回りに同時に動き始めます。
(1) 点P、Qが初めて出会うのは何秒後ですか。
(2) 点P、Qが初めて辺ABと平行になるのは何秒後ですか。
(3) 点P、Qが初めて同時にもとの位置に戻るのは何秒後ですか。

(1)
出会うまでに点P、Qが辺3つ分を動くので、48×3÷(4+8)=12秒後に頂点Bで出会う。(答え)12秒後
(2)
点Pが頂点Cに、点Qが頂点Dに来た時に辺ABと平行になる。よって、48×2÷4=24秒後。(答え)24秒後
(3)
動きの速い点Qから見ると、点Qが1周してもとの位置に戻った時、点Pは1周の半分の頂点Cにいる。よって、点Qが2周してもとの位置に戻った時、点Pは1周してもとの位置に戻る。点P、Qが初めて同時にもとの位置に戻るのは48×8÷8=48秒後。(答え)48秒後
ではまた~