問題
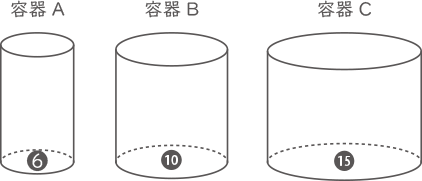
円柱の形をした3つの容器A,B,Cがあり,AとBとCの底面積の比は6:10:15です。
(1) A,B,Cにそれぞれ水が入っています。Aに入っている水の量の1/5をBに移し,その後,Bに入っている水の量の1/6をCに移すと,A,B,Cに入っている水の高さは同じになりました。A,B,Cにはじめに入っていた水の量の比を,もっとも簡単な整数の比で表しなさい。
(2) (1)の水を捨て,新たにA,B,Cにそれぞれ水を入れなおしました。その後, Cに入っている水の量の2/7をAへ,残りの水の量の1/5をBへ移しました。次に,Aに入っている水の量の1/4をBへ移し,さらにBに入っている水の量の1/6をCへ移すと,A,B,Cに入っている水の量は等しくなりました。A,B,Cに水を入れなおしたときの水の高さの比を,もっとも簡単な整数の比で表しなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
円柱の形をした3つの容器A,B,Cがあり,AとBとCの底面積の比は6:10:15です。
(1) A,B,Cにそれぞれ水が入っています。Aに入っている水の量の1/5をBに移し,その後,Bに入っている水の量の1/6をCに移すと,A,B,Cに入っている水の高さは同じになりました。A,B,Cにはじめに入っていた水の量の比を,もっとも簡単な整数の比で表しなさい。
(2) (1)の水を捨て,新たにA,B,Cにそれぞれ水を入れなおしました。その後, Cに入っている水の量の2/7をAへ,残りの水の量の1/5をBへ移しました。次に,Aに入っている水の量の1/4をBへ移し,さらにBに入っている水の量の1/6をCへ移すと,A,B,Cに入っている水の量は等しくなりました。A,B,Cに水を入れなおしたときの水の高さの比を,もっとも簡単な整数の比で表しなさい。

(1)
2回移し終えた後の水の高さが同じになるので、水の量の比は底面積比と同じA:B:C=6:10:15となる。
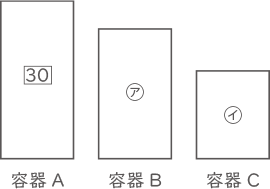
容器Aの水量を$ \fbox{30} $(5と6の最小公倍数)、
容器Bの水量を㋐、
容器Cの水量を㋑、
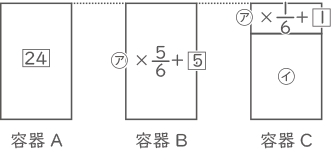
とする。容器Aの水量の$ \displaystyle \frac{1}{5} $にあたる$ \fbox{6} $を容器Bに移す。容器Aの水量は$ \fbox{24} $、
容器Bの水量は㋐+$ \fbox{6} $、
容器Cの水量は㋑、
になった。容器Bの$ \displaystyle \frac{1}{6} $にあたる㋐×$ \displaystyle \frac{1}{6} $+$ \fbox{1} $を容器Cに移す。容器Aの水量は$ \fbox{24} $、
容器Bの水量は㋐×$ \displaystyle \frac{5}{6} $+$ \fbox{5} $、
容器Cの水量は㋐×$ \displaystyle \frac{1}{6} $+$ \fbox{1} $+㋑、
になり、3つの容器とも高さが同じになった。
容器Aの水量を$ \fbox{24} $=⑥、
容器Bの水量を㋐×$ \displaystyle \frac{5}{6} $+$ \fbox{5} $=⑩、
容器Cの水量を㋐×$ \displaystyle \frac{1}{6} $+$ \fbox{1} $+㋑=⑮、
として、
容器Aの式より①=$ \fbox{4} $、
容器Bは㋐×$ \displaystyle \frac{5}{6} $+$ \fbox{5} $=$ \fbox{40} $、㋐×$ \displaystyle \frac{5}{6} $=$ \fbox{35} $、㋐=$ \fbox{42} $
容器Cは$ \fbox{42} $×$ \displaystyle \frac{1}{6} $+$ \fbox{1} $+㋑=$ \fbox{60} $ 、$ \fbox{8} $+㋑=$ \fbox{60} $ 、㋑=$ \fbox{52} $はじめに入っていた水の量の比は、$ \fbox{30} $:$ \fbox{42} $:$ \fbox{52} $=15:21:26となる。
(答え) 15:21:26
(2)
容器Aの水量を㋒、
容器Bの水量を㋓、
容器Cの水量を$ \fbox{420} $(7,5,4,6の最小公倍数)、
とする。容器Cの水量の$ \displaystyle \frac{2}{7} $にあたる$ \fbox{120} $を容器Aに移す。容器Aの水量は㋒+$ \fbox{120} $、
容器Bの水量は㋓、
容器Cの水量は$ \fbox{300} $、
になった。容器Cの残りの水量の$ \displaystyle \frac{1}{5} $にあたる60を容器Bに移す。容器Aの水量は㋒+$ \fbox{120} $、
容器Bの水量は㋓+$ \fbox{60} $、
容器Cの水量は$ \fbox{240} $、
になった。容器Aの水量の$ \displaystyle \frac{1}{4} $にあたる(㋒×$ \displaystyle \frac{1}{4} $+$ \fbox{30} $)を容器Bに移す。容器Aの水量は㋒×$ \displaystyle \frac{3}{4} $+$ \fbox{90} $、
容器Bの水量は㋒×$ \displaystyle \frac{1}{4} $+㋓+$ \fbox{90} $、
容器Cの水量は$ \fbox{240} $、
になった。容器Bの水量の$ \displaystyle \frac{1}{6} $にあたる(㋒×$ \displaystyle \frac{1}{24} $+㋓×$ \displaystyle \frac{1}{6} $+$ \fbox{15} $)を容器Cに移す。容器Aの水量は㋒×$ \displaystyle \frac{3}{4} $+$ \fbox{90} $、
容器Bの水量は㋒×$ \displaystyle \frac{5}{24} $+㋓×$ \displaystyle \frac{5}{6} $+$ \fbox{75} $ 、
容器Cの水量は ㋒×$ \displaystyle \frac{1}{24} $+㋓×$ \displaystyle \frac{1}{6} $+$ \fbox{255} $ 、
になり、3つの容器とも水の量が同じになった。容器Aの水量を㋒×$ \displaystyle \frac{18}{24} $+$ \fbox{90} $=①・・・(式1)
容器Bの水量を㋒×$ \displaystyle \frac{5}{24} $+㋓×$ \displaystyle \frac{5}{6} $+$ \fbox{75} $=①・・・(式2)
容器Cの水量を ㋒×$ \displaystyle \frac{1}{24} $+㋓×$ \displaystyle \frac{1}{6} $+$ \fbox{255} $=①・・・(式3)
として、
㋒×$ \displaystyle \frac{5}{24} $+㋓×$ \displaystyle \frac{5}{6} $+$ \fbox{1275} $=⑤・・・(式3)×5
㋒×$ \displaystyle \frac{5}{24} $+㋓×$ \displaystyle \frac{5}{6} $+$ \fbox{75} $=①・・・(式2)
差は1200 =④、①=$ \fbox{300} $(式1)から
㋒×$ \displaystyle \frac{18}{24} $+$ \fbox{90} $=$ \fbox{300} $、計算すると㋒=$ \fbox{280} $(式3)から
$ \fbox{280} $×$ \displaystyle \frac{1}{24} $+㋓×$ \displaystyle \frac{1}{6} $+$ \fbox{255} $=$ \fbox{300} $、計算すると㋓=$ \fbox{200} $水を入れなおしたときの水の量の比は、
A:B:C=㋒:㋓:$ \fbox{420} $=$ \fbox{280} $:$ \fbox{200} $:$ \fbox{420} $=14:10:21
水を入れなおしたときの水の高さの比は、
A:B:C=$ \displaystyle \frac{14}{6} $:$ \displaystyle \frac{10}{10} $:$ \displaystyle \frac{21}{15} $=35:15:21(答え) 35:15:21