問題
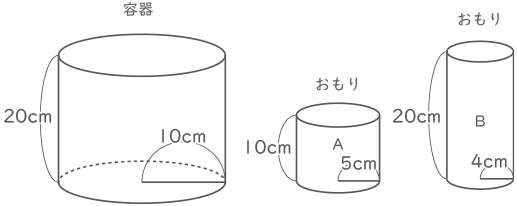
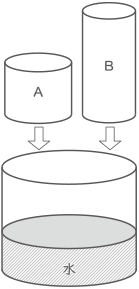
下の図のような,底面の半径が10cm,高さ20cmの円柱の容器と,底面の半径が5cm,高さ10cmの円柱のおもりA, 底面の半径が4cm,高さ20cmの円柱のおもりBがあります。
様々な高さまで水が入った容器におもりAとBを入れたときの水位(水面の高さ)の変化について考えます。ただし,容器の底におもりの底面がぴったり重なるようにおもりを入れます。また,容器の厚さは考えないものとします。
小数点以下がある場合は,四捨五入をして小数第1位まで答えなさい。
(1) ある高さまで水が入った容器にA とBのおもりを入れたところ,下の図のように容器はちょうど満水になりました。容器にはもともと何cmの高さまで水が入っていたか答えなさい。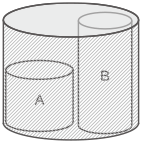
(2) 6cmの高さまで水の入った容器にAとBのおもりを,まずA,その後でBの順に入れました。
① Aのおもりを入れると水位は何cmになるか答えなさい。
② Bのおもりを入れると水位は何cmになるか答えなさい。
(3) ある高さまで水が入った容器に,A,Bの順におもりを入れたときとB,Aの順におもりを入れたときとでは,2つ目のおもりを入れる前と後の水位の差が等しくなりました。容器にはもともと何cmの高さまで水が入っていたか答えなさい。求め方も書きなさい。ただし,水はあふれなかったものとします。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
下の図のような,底面の半径が10cm,高さ20cmの円柱の容器と,底面の半径が5cm,高さ10cmの円柱のおもりA, 底面の半径が4cm,高さ20cmの円柱のおもりBがあります。

様々な高さまで水が入った容器におもりAとBを入れたときの水位(水面の高さ)の変化について考えます。ただし,容器の底におもりの底面がぴったり重なるようにおもりを入れます。また,容器の厚さは考えないものとします。

小数点以下がある場合は,四捨五入をして小数第1位まで答えなさい。
(1) ある高さまで水が入った容器にA とBのおもりを入れたところ,下の図のように容器はちょうど満水になりました。容器にはもともと何cmの高さまで水が入っていたか答えなさい。

(2) 6cmの高さまで水の入った容器にAとBのおもりを,まずA,その後でBの順に入れました。
① Aのおもりを入れると水位は何cmになるか答えなさい。
② Bのおもりを入れると水位は何cmになるか答えなさい。(3) ある高さまで水が入った容器に,A,Bの順におもりを入れたときとB,Aの順におもりを入れたときとでは,2つ目のおもりを入れる前と後の水位の差が等しくなりました。容器にはもともと何cmの高さまで水が入っていたか答えなさい。求め方も書きなさい。ただし,水はあふれなかったものとします。

(1)
容器の容量:10×10×円周率×20
おもりAの体積:5×5×円周率×10
おもりBの体積:4×4×円周率×20
2つのおもりが入ったときの容器の残り容量=(10×10×円周率×20)-(5×5×円周率×10)-(4×4×円周率×20)=1430×円周率
容器にもともと入っていた水の高さ=1430×円周率÷(10×10×円周率)=14.3cm(答え) 14.3cm
(2)ー①
6cmの高さまでの水量:10×10×円周率×6・・・(ア)
おもりAを入れて水を10cmまで入れた水量:(100-25)×円周率×10・・・(イ)
(ア)<(イ)なので水はおもりAの高さを超えない。
10×10×円周率×6÷{(100-25)×円周率}=600÷75=8(答え) 8cm
(2)ー②
2つのおもりを入れた状態で考える。
10cmまでの底面積:(100-25-16)×円周率
10cmより上の底面積:(100-16)×円周率
10cmまでに入る水量:(100-25-16)×円周率×10=590×円周率
10cmより上に入る水量:10×10×円周率×6-590×円周率=10×円周率
10cmよりどのくらい上になるか:10×円周率÷{(100-16)×円周率}=10÷84=0.1$ \displaystyle \cancel{1} $…→0.1
10+0.1=10.1(答え) 10.1cm
(3)
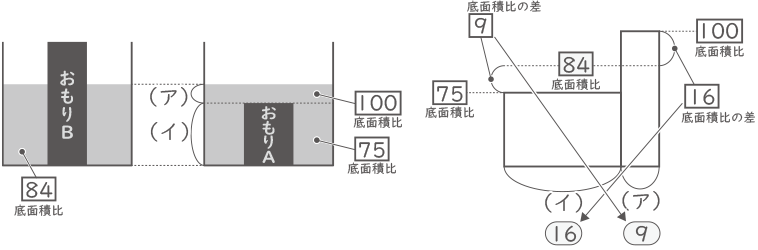
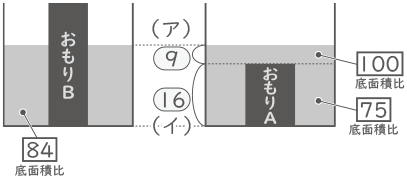
水があふれないのであれば、おもりA、Bのどちらから入れても、2つ入れた後の水の高さは同じ。前後の水位の差が同じという事は、おもりAだけが入っている場合の水の高さと、おもりBだけが入っている場合の水の高さが同じという事。【もし、おもりAの高さがおもりBと同じであれば水位の差は等しくならないので、おもりAだけを入れた場合は、水位はおもりAより上になるとわかる。】
底面積を比で考える。
おもりAだけが入ったときの底面積:(100-25)×円周率・・・$ \fbox{75} $
おもりBだけが入ったときの底面積:(100-16)×円周率・・・$ \fbox{84} $
おもりが入っていないときの底面積:100×円周率・・・$ \fbox{100} $
おもりAだけを入れた場合のおもりより上の水位を(ア)、それ以外を(イ)とする。面積図を利用すると、たすき掛けの形で(ア):(イ)=⑨:⑯となる。
【(ア)、(イ)の比が分かったので次に(イ)の高さがおもりA無しでどのくらい下がるか求める。】

(イ)の水は底面積$ \fbox{75} $で⑯の高さであれば、底面積$ \fbox{100} $では⑫(=$ \fbox{75} $×⑯÷$ \fbox{100} $)。
よって、おもりAを取り除いた底面積$ \fbox{100} $のとき、(ア)にあった水量と(イ)にあった水量の和の高さは㉕から㉑(=⑨+⑫)になる。もともとの(イ)の高さ⑯が10cmなので㉑は10cm×$ \displaystyle \frac{21}{16} $=13.1$\cancel{2}$$\cancel{5}$ → 13.1
(答え) 13.1cm