問題
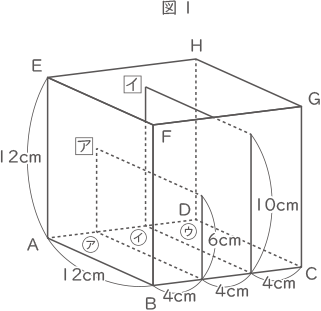
図1のような,ふたのない1辺12cmの立方体の容器が水平な床(ゆか)に置かれている。この立方体には,図1のように,高さ6cmと10cmの仕切り板 $ \fbox{ア} $ $ \fbox{イ} $ が,底面ABCDを3等分する位置にまっすぐ取り付けられている。仕切られた底面を㋐,㋑,㋒とし,仕切り板の厚さは考えないものとする。
また,図2は面FBCGを正面にして見た図である。
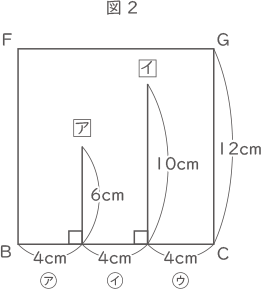
(1) 容器が空の状態で,㋐の真上から水を毎秒48cm3ずつ入れたとき,容器の中の水がいっぱいになるのは何秒後ですか。
(2) 容器が空の状態で,㋒の真上から水を毎秒48cm3ずつ入れたとき,㋐の部分の水面の高さが底から2cmになるのは何秒後ですか。
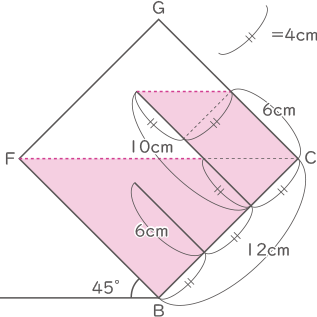
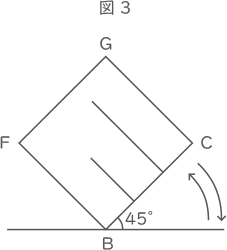 (3) 容器を水でいっぱいに満たし,図3のように,辺ABを床につけたまま,静かに容器を45°かたむけて水をこぼし,もとにもどす動作を行った。この動作を行った後,容器に残っている水の量を求めなさい。
(3) 容器を水でいっぱいに満たし,図3のように,辺ABを床につけたまま,静かに容器を45°かたむけて水をこぼし,もとにもどす動作を行った。この動作を行った後,容器に残っている水の量を求めなさい。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
図1のような,ふたのない1辺12cmの立方体の容器が水平な床(ゆか)に置かれている。この立方体には,図1のように,高さ6cmと10cmの仕切り板 $ \fbox{ア} $ $ \fbox{イ} $ が,底面ABCDを3等分する位置にまっすぐ取り付けられている。仕切られた底面を㋐,㋑,㋒とし,仕切り板の厚さは考えないものとする。
また,図2は面FBCGを正面にして見た図である。

(1) 容器が空の状態で,㋐の真上から水を毎秒48cm3ずつ入れたとき,容器の中の水がいっぱいになるのは何秒後ですか。
(2) 容器が空の状態で,㋒の真上から水を毎秒48cm3ずつ入れたとき,㋐の部分の水面の高さが底から2cmになるのは何秒後ですか。
 (3) 容器を水でいっぱいに満たし,図3のように,辺ABを床につけたまま,静かに容器を45°かたむけて水をこぼし,もとにもどす動作を行った。この動作を行った後,容器に残っている水の量を求めなさい。
(3) 容器を水でいっぱいに満たし,図3のように,辺ABを床につけたまま,静かに容器を45°かたむけて水をこぼし,もとにもどす動作を行った。この動作を行った後,容器に残っている水の量を求めなさい。(1)
12×12×12÷48=36(答え) 36秒後
(2)
㋒の高さ10cmまでの容積=4×12×10=480cm3
㋑の高さ6cmまでの容積=4×12×6=288cm3
㋐の高さ2cmまでの容積=4×12×2=96cm3
(480+288+96)÷48=18(答え) 18秒後
 (3)
(3)
横から見たときの残った水は図の通りで、色の付いている部分の面積を求めると、
㋒の部分は(10+6)×4÷2=32cm2
㋐と㋑の部分は(12+4)×8÷2=64cm2
合わせて96cm2で、奥行12cmなので求める水量は
96×12=1152cm3(答え) 1152cm3


 (3)
(3)








