問題
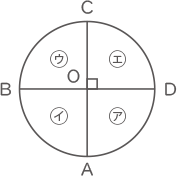
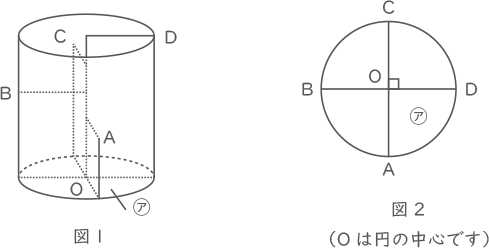
図1のように,円柱の容器の中に4つの仕切りが底面と垂直に立てられています。図2は円柱を上から見たものです。㋐の真上から水を一定の割合で入れ始めました。水が仕切りA,B,Cを超えたのは水を入れ始めてそれぞれ3分後,8分後,17分後でした。また,28分後に円柱は水でいっぱいになりました。仕切りA,B,C,Dの高さの比を最も簡単な整数の比で表しなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
図1のように,円柱の容器の中に4つの仕切りが底面と垂直に立てられています。図2は円柱を上から見たものです。㋐の真上から水を一定の割合で入れ始めました。水が仕切りA,B,Cを超えたのは水を入れ始めてそれぞれ3分後,8分後,17分後でした。また,28分後に円柱は水でいっぱいになりました。仕切りA,B,C,Dの高さの比を最も簡単な整数の比で表しなさい。


円柱の底面積を㋐,㋑,㋒,㋓とすると、それぞれの底面積は同じ大きさ。
底面積㋐部分が仕切りAまで水がたまるまでに3分・・・❶
底面積㋐+㋑部分が仕切りAまで水がたまるまでに6分(❶の倍の時間)・・・❷
底面積㋐+㋑部分が仕切りBまで水がたまるまでに8分・・・❸
❷と❸から仕切りの高さの比はA:B=6:8=3:4底面積㋐+㋑+㋒部分が仕切りBまで水がたまるまでに12分(=8+4)(❸の体積の半分は4分間でたまる)・・・❹
底面積㋐+㋑+㋒部分が仕切りCまで水がたまるまでに17分・・・❺
❹と❺から仕切りの高さの比はB:C=12:17底面積㋐+㋑+㋒+㋓部分が仕切りCまで水がたまるまでに$ \displaystyle \frac{68}{3} $分(=17+$ \displaystyle \frac{17}{3} $)(❺の体積の$ \displaystyle \frac{1}{3} $は$ \displaystyle \frac{17}{3} $分でたまる)・・・❻
底面積㋐+㋑+㋒+㋓部分が仕切りDまで水がたまるまでに28分・・・❼
❻と❼から仕切りの高さの比はC:D=$ \displaystyle \frac{68}{3} $:28=17:21A:B=3:4=9:12
B:C=12:17
C:D=17:21A:B:C:D=9:12:17:21
(答え) A:B:C:D=9:12:17:21