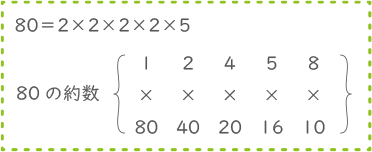約数-3-2（暁星中学2022/約束記号は単純だが約数の数を求めるのに時間が掛かりそう）

問題

解答

 解答を開く

 

1以上の整数Xに対して、X の約数の個数を記号[X]で表すことにします。

（1） 次の値を求めなさい。
① [80]　② [81]

（2） 1以上2022以下の整数Yに対して、[Y]＝3となるYの個数を求めなさい。
（3） 1以上2022以下の整数Zに対して、[Z]= 9となる最大の整数Zの値を求めなさい。

 

---

 

（1）―①
80を素因数分解すると80＝2×2×2×2×5
2が4個、5が１個なので約数の数は（4＋1）×（1＋1）＝10

（答え）　10

 

（1）―②
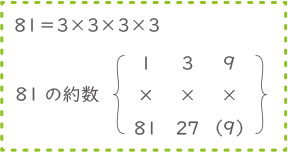
81を素因数分解すると81＝3×3×3×3
3が4個なので約数の数は4＋1＝5

（答え）　5

 

（2）
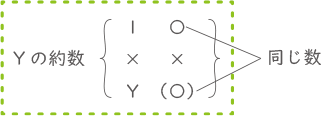
下図の数Yについて、約数が「１」と「自分自身Y」ともう一つだけの時に[Y]＝3となる。この条件を満たす〇は素数。
1×1＝1と45×45＝2025（＞2022）より、1から44の中で素数を探すと、
2,3,5,7,11,13,17,19,23,29,31,37,41,43の14個。

（答え）　14個

 

（3）
約数の個数が9個の数とは、約数の個数を求める式が8＋1＝9か3×3＝9となる数。
（約数の数を求める方法については解説ページを参照しましょう。）

【8＋1＝9のとき】
8（＝9－1）回同じ数をかけ合わせてできる数。
（□×□×□×□×□×□×□×□＝求める数）
2×2×2×2×2×2×2×2＝256
3×3×3×3×3×3×3×3＝6561
この形での条件に当てはまる数はない。

【3×3＝9のとき】
ある数を2（＝3－1）回かけ合わせ、別のある数を2（＝3－1）回かけ合わせ、その積でできる数。
（□×□×△×△＝求める数）
（□×△）×（□×△）の形にして、□と△が素数となる数を大きい順に探す。
45×45＝5×9×5×9・・・×
44×44＝4×11×4×11・・・×
43×43＝・・・×
42×42＝2×21×2×21・・・×
41×41＝・・・×
40×40＝4×10×4×10・・・×
39×39＝3×13×3×13＝1521・・・〇

（答え）　1521