問題
次の問いに答えなさい。ただし、円周率は3.14とします。
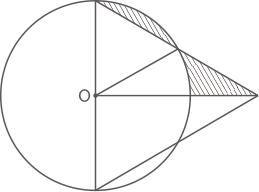
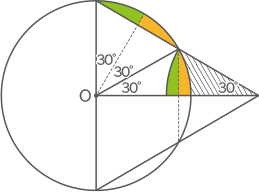
(1) 下の図は、円と正三角形を、正三角形の一辺が円の中心Oを通るように重ねたものです。円の半径が3cmのとき、斜線部の面積の和を求めなさい。
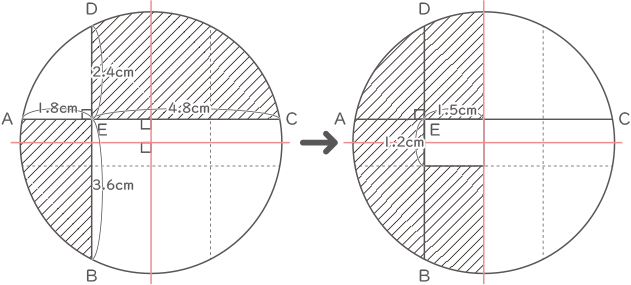
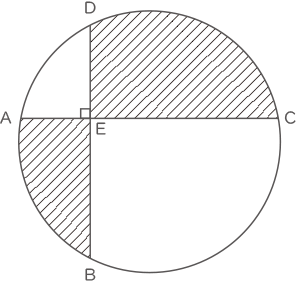
(2) 下の図において、ACとBDは垂直で、AE=1.8cm、BE=3.6cm、CE=4.8cm、DE=2.4cmです。円の面積が36cm2であるとき、斜線部の面積の和を求めなさい。
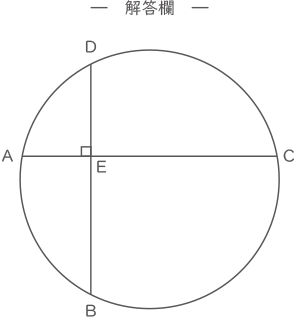
ただし、解答用紙にある図を用いて、考え方を説明しなさい。
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 <オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます!しかも授業料は【格安】>
解答
- 解答を開く
-
次の問いに答えなさい。ただし、円周率は3.14とします。
(1) 下の図は、円と正三角形を、正三角形の一辺が円の中心Oを通るように重ねたものです。円の半径が3cmのとき、斜線部の面積の和を求めなさい。

(2) 下の図において、ACとBDは垂直で、AE=1.8cm、BE=3.6cm、CE=4.8cm、DE=2.4cmです。円の面積が36cm2であるとき、斜線部の面積の和を求めなさい。
ただし、解答用紙にある図を用いて、考え方を説明しなさい。
 (1)
(1)
色の付いた面を移動すると、求める面積は中心角30°のおうぎ形の面積とおなじとなる。
3×3×3.14×$ \displaystyle \frac{30}{360} $=2.355cm2(答え) 2.355cm2
(2)
円の中心を通る2つの赤線に線対象な破線を追加する。
同じ面積のところを移動する。
求める面積=36÷2-1.5×1.2=16.2cm2
(答え) 16.2cm2

 (1)
(1)