問題
問題(図形を回転させた時に辺の通過する部分の面積)
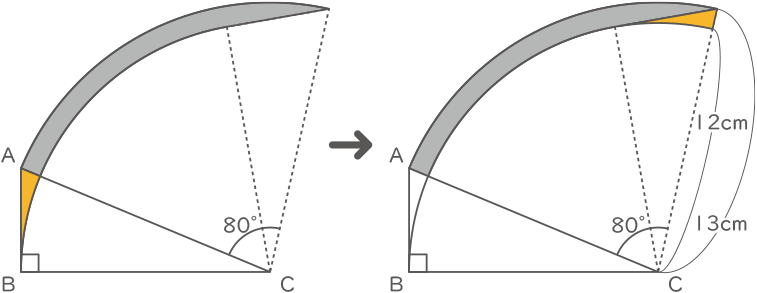
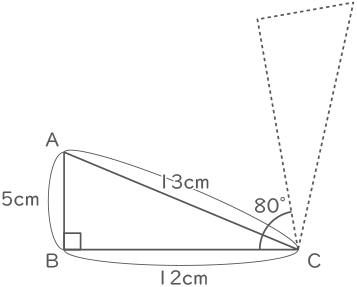
図の様な直角三角形ABCを、その頂点Cを中心として時計回りに80°回転させたときにできる、辺ABが通過する部分の面積を求めなさい。ただし、円周率は3.14とします。
自宅学習で身につける、難関中学への合格力「Z会」
4.02
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
図の様な直角三角形ABCを、その頂点Cを中心として時計回りに80°回転させたときにできる、辺ABが通過する部分の面積を求めなさい。ただし、円周率は3.14とします。

半径13cm(辺AC)で中心角80°のおうぎ形の面積から、半径12cm(辺BC)で中心角80°のおうぎ形の面積を引いた値が答えなので、
13×13×3.14×$ \displaystyle \frac{80}{360} $-12×12×3.14×$ \displaystyle \frac{80}{360} $=17$ \displaystyle \frac{4}{9} $
(答え)17$ \displaystyle \frac{4}{9} $cm2
ではまた~