問題
開成君の時計はつねに正しい時刻より5分遅れた時刻を指します。この時計について,次の問いに答えなさい。
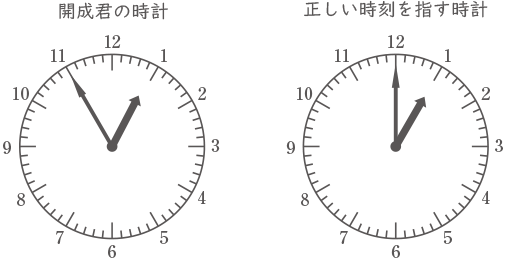
(1) 開成君の時計の長針と正しい時刻を指す時計の短針が同じ位置にくる場合を考えます。正しい時刻で1時を過ぎたあと,初めてそのようになるのは何時何分ですか。正しい時刻で答えなさい。
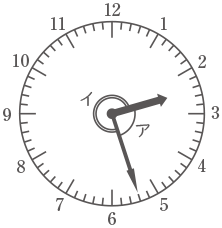
正しい時刻を指す時計の短針と長針の間にできる角の大きさをa,開成君の時計の短針と長針の間にできる角の大きさをbという文字で表すことにします。ただし,短針と長針の間にできる角というのは,たとえば次の図のような例でいうと,短針と長針によってできる角ア,イのうち,角の大きさが180° 以下である角アのほうを指すものとします。
(2) 正しい時刻で1時を過ぎたあと(1)の時刻までの間で,a とbが等しくなるのは何時何分ですか。正しい時刻で答えなさい。
(3) 正しい時刻で1時を過ぎたあと(1)の時刻までの間で, aがbの2倍になる時刻をA とし,(1)の時刻を過ぎてから初めてaがbの2倍になる時刻をBとします。時刻Aから時刻Bまでの時間は何分何秒ですか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
開成君の時計はつねに正しい時刻より5分遅れた時刻を指します。この時計について,次の問いに答えなさい。

(1) 開成君の時計の長針と正しい時刻を指す時計の短針が同じ位置にくる場合を考えます。正しい時刻で1時を過ぎたあと,初めてそのようになるのは何時何分ですか。正しい時刻で答えなさい。
正しい時刻を指す時計の短針と長針の間にできる角の大きさをa,開成君の時計の短針と長針の間にできる角の大きさをbという文字で表すことにします。ただし,短針と長針の間にできる角というのは,たとえば次の図のような例でいうと,短針と長針によってできる角ア,イのうち,角の大きさが180° 以下である角アのほうを指すものとします。

(2) 正しい時刻で1時を過ぎたあと(1)の時刻までの間で,a とbが等しくなるのは何時何分ですか。正しい時刻で答えなさい。
(3) 正しい時刻で1時を過ぎたあと(1)の時刻までの間で, aがbの2倍になる時刻をA とし,(1)の時刻を過ぎてから初めてaがbの2倍になる時刻をBとします。時刻Aから時刻Bまでの時間は何分何秒ですか。
(1)
60÷(6-0.5)=10$ \displaystyle \frac{10}{11} $分
正しい時刻では1時10$ \displaystyle \frac{10}{11} $分(答え) 1時10$ \displaystyle \frac{10}{11} $分
(2)
正しい時計で1時の直後に長針と短針が重なる時刻を求めると、
30÷(6-0.5)=5$ \displaystyle \frac{5}{11} $
1時5$ \displaystyle \frac{5}{11} $分。
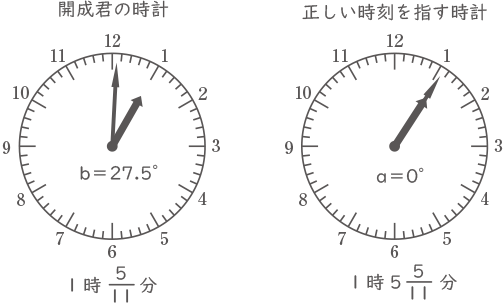
そのときの開成君の時計は5分遅れなので1時$ \displaystyle \frac{5}{11} $分。
長針と短針の進む差は1分に5.5°なので$ \displaystyle \frac{5}{11} $分では2.5°の差。正しい時計の長針と短針が重なる(a=0°)とき、開成君の時計の長針と短針の角度bは30-2.5=27.5°。
求める時刻はこの直後のa=b=13.75°になったとき。
13.75°の差がでるのは13.75÷5.5=2.5分後。正しい時刻で1時5$ \displaystyle \frac{5}{11} $分+2.5分=1時7$ \displaystyle \frac{21}{22} $分。
(答え) 1時7$ \displaystyle \frac{21}{22} $分
(3)
【時刻Aを求める】
1時から(1)の時刻まででa=b×2となるのは、(2)の27.5°を使って、
bが(27.5×$ \displaystyle \frac{1}{3} $)°になったとき。
そのときaは27.5-(27.5×$ \displaystyle \frac{1}{3} $)=27.5×$ \displaystyle \frac{2}{3} $
27.5×$ \displaystyle \frac{2}{3} $÷5.5=3$ \displaystyle \frac{1}{3} $分よって、時刻Aは1時5$ \displaystyle \frac{5}{11} $分+3$ \displaystyle \frac{1}{3} $分=1時8$ \displaystyle \frac{26}{33} $分。
【時刻Bを求める】
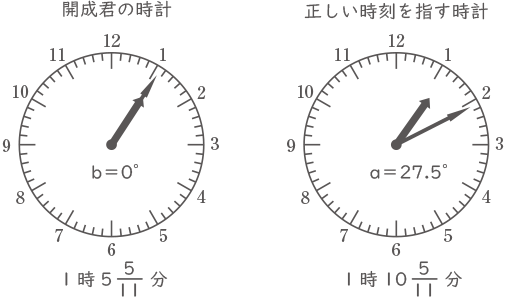
開成君の時計の長針と短針が重なる時刻の1時5$ \displaystyle \frac{5}{11} $分のとき、
正しい時計の時刻は1時10$ \displaystyle \frac{5}{11} $分で、a=27.5°となる。
開成君の時計のbが0°から□°進むと、正しい時計のaは(27.5+□)°になる。
□=①
27.5+□=②
となる□を消去算で求めると
□+□=②
27.5+□=②
なので、□+□=27.5+□
□=27.5°
27.5°進む時間は27.5÷5.5=5分
よって、時刻Bは1時10$ \displaystyle \frac{5}{11} $分+5分=1時15$ \displaystyle \frac{5}{11} $分。【時刻Aから時刻Bまでの時間】
1時15$ \displaystyle \frac{5}{11} $分-1時8$ \displaystyle \frac{26}{33} $分=6$ \displaystyle \frac{2}{3} $分=6分40秒(答え) 6分40秒