問題
12時から13時の間での短針と長針の関係について下記の問に答えなさい。
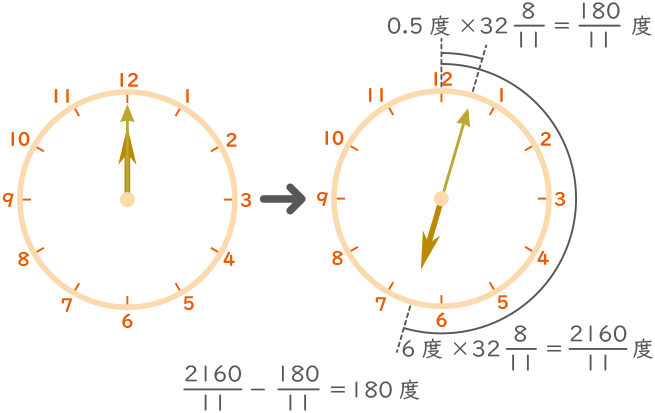
(1)短針と長針の角度が180°になるのは12時何分ですか。
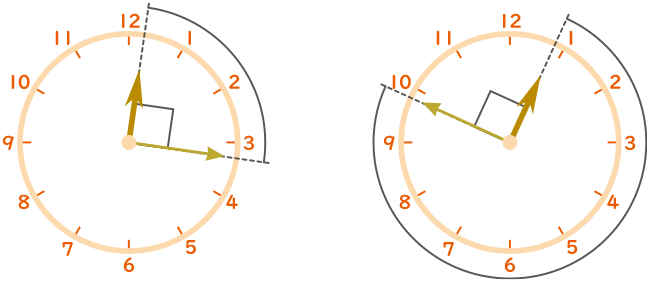
(2)短針と長針が垂直になるのは12時何分ですか。2つ答えなさい。
- ポイント・ヒントを開く
-
短針は1分間に0.5度、長針は1分間に6度進む。短針と長針の進む差は5.5度。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
12時から13時の間での短針と長針の関係について下記の問に答えなさい。
(1)短針と長針の角度が180°になるのは12時何分ですか。
(2)短針と長針が垂直になるのは12時何分ですか。2つ答えなさい。
(1)
短針と長針は1分間に5.5度離れていくので、角度0°(12時)から角度180°になるには、180÷5.5=32\( \displaystyle \frac{8}{11} \)分かかる。よって12時32\( \displaystyle \frac{8}{11} \)分。
(答え)12時32\( \displaystyle \frac{8}{11} \)分
(2)
短針と長針は1分間に5.5度離れていくので、角度0°(12時)から角度90°になるには、90÷5.5=16\( \displaystyle \frac{4}{11} \)分かかる。よって1つ目の角度は12時16\( \displaystyle \frac{4}{11} \)分。
角度0°(12時)から角度270°になるには、270÷5.5=49\( \displaystyle \frac{1}{11} \)分かかる。よって2つ目の角度は12時49\( \displaystyle \frac{1}{11} \)分。
(答え)12時16\( \displaystyle \frac{4}{11} \)分と12時49\( \displaystyle \frac{1}{11} \)分