問題
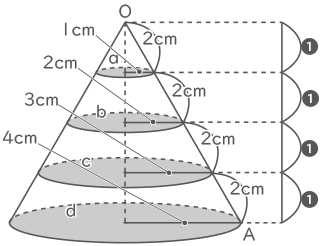
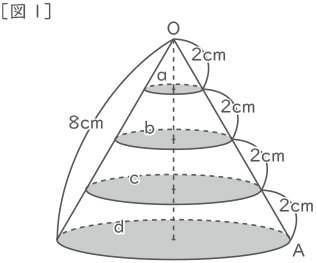
図1 のように,底面の半径が4cmでOAの長さが8cmの,粘土(ねんど)でできた円すいがあります。この円すいを,底面に平行で等間隔(とうかんかく)な3つの平面で4つのブロックに切り分け,いちばん小さいブロックから大きい方へ順にa,b, c, dと呼ぶことにします。このとき,次の問いに答えなさい。
(1) ブロックbとdの体積の比,および,表面積の比を求めなさい。
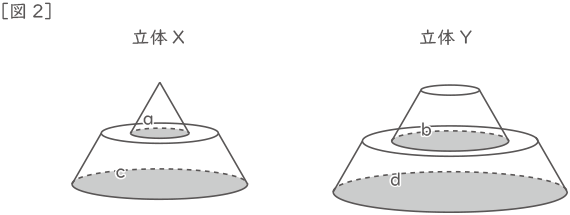
(2) ブロックa,cを図2のように積み上げて立体を作りXと呼ぶことにします。同じように,ブロックb,dを積み上げて立体を作りYと呼ぶことにします。立体XとYの体積の比,および,表面積の比を求めなさい。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
図1 のように,底面の半径が4cmでOAの長さが8cmの,粘土(ねんど)でできた円すいがあります。この円すいを,底面に平行で等間隔(とうかんかく)な3つの平面で4つのブロックに切り分け,いちばん小さいブロックから大きい方へ順にa,b, c, dと呼ぶことにします。このとき,次の問いに答えなさい。

(1) ブロックbとdの体積の比,および,表面積の比を求めなさい。
(2) ブロックa,cを図2のように積み上げて立体を作りXと呼ぶことにします。同じように,ブロックb,dを積み上げて立体を作りYと呼ぶことにします。立体XとYの体積の比,および,表面積の比を求めなさい。
各ブロックの底面の半径は三角形の相似より求まる。
底面半径4cmのときに高さを❹とすれば、
❸のとき3cm、
❷のとき2cm、
❶のとき1cmとなる。
(円周率も高さも与えられていないが求めるものは比であり、相似な立体として考えていけばよい。)
円すいaの底面積=1×1×円周率・・・(①)とする
円すいaの側面積=$ \displaystyle \frac{1}{2} $×2×2×円周率・・・底面積の倍なので(①×2)とする
円すいaの体積=1×1×円周率×❶・・・($ \fbox{1} $)とする円すい(a+b)の底面積は(①)×2×2=①×4
円すい(a+b)の側面積は(①×2)×2×2=①×8
円すい(a+b)の体積は($ \fbox{1} $)×2×2×2=$ \fbox{1} $×8円すい(a+b+c)の底面積は(①)×3×3=①×9
円すい(a+b+c)の側面積は(①×2)×3×3=①×18
円すい(a+b+c)の体積は($ \fbox{1} $)×3×3×3=$ \fbox{1} $×27円すい(a+b+c+d)の底面積は(①)×4×4=①×16
円すい(a+b+c+d)の側面積は(①×2)×4×4=①×32
円すい(a+b+c+d)の体積は($ \fbox{1} $)×4×4×4=$ \fbox{1} $×64(1)
ブロックbの体積=$ \fbox{1} $×8-$ \fbox{1} $=$ \fbox{1} $×7
ブロックdの体積=$ \fbox{1} $×64-$ \fbox{1} $×27=$ \fbox{1} $×37
ブロックbの体積:ブロックdの体積=($ \fbox{1} $×7):($ \fbox{1} $×37)=7:37ブロックbの表面積=①+①×4+(①×8-①×2)=①×11
ブロックdの表面積=①×9+①×16+(①×32-①×18)=①×39
ブロックbの表面積:ブロックdの表面積=(①×11):(①×39)=11:39(答え) 体積の比は7:37、 表面積の比は11:39
(2)
立体X(aとc)の体積=($ \fbox{1} $)+($ \fbox{1} $×27-$ \fbox{1} $×8)=$ \fbox{1} $×20
立体Y(bとd)の体積=円すい(a+b+c+d)の体積-立体X(aとc)の体積=$ \fbox{1} $×64-$ \fbox{1} $×20=$ \fbox{1} $×44
立体X(aとc)の体積:立体Y(bとd)の体積=$ \fbox{1} $×20:$ \fbox{1} $×44=5:11立体X(aとc)の表面積=①×2+(①×4-①)+(①×18-①×8)+①×9=①×24
立体Y(bとd)の表面積=①+(①×8-①×2)+(①×9-①×4)+(①×32-①×18)+①×16=①×42
立体X(aとc)の表面積:立体Y(bとd)の表面積=①×24:①×42=24:42=4:7(答え) 体積の比は5:11、 表面積の比は4:7