問題
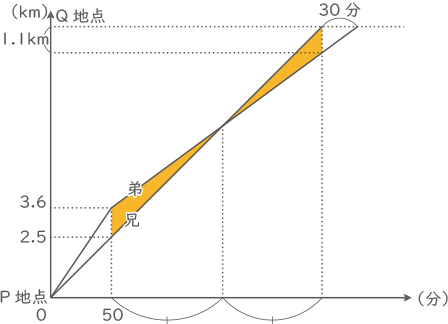
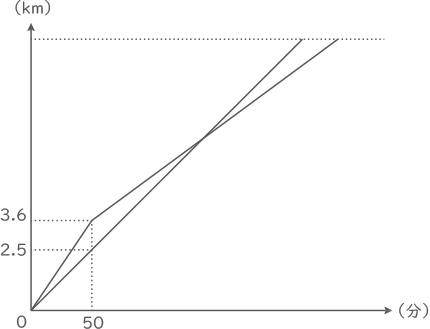
ある日、兄と弟2人がP地点からQ地点まで同じ道を歩きました。弟は途中1回だけ速さを変え、兄は一定の速さで進んだところ、兄の方が30分早くQ地点に着きました。弟が速さを変えてから兄に追い抜かれるまでの時間と追い抜かれてから兄がQ地点に着くまでの時間は同じでした。下のグラフはその日に2人が出発してからQ地点に着くまでの時間と道のりを表したものです。
(1) 弟がQ地点に着いたときの速さは、時速何kmか求めなさい。
(2) P地点からQ地点までの距離を求めなさい。
(3) 次の日、弟は(1)の速さでQ地点からP地点まで歩きました。弟が出発した後に兄はQ地点を出発し、前日と同じ速さで歩きました。弟がP地点に着いたときの兄との距離の差は、兄が出発したときの弟との差の$ \displaystyle \frac{5}{11} $倍でした。このとき、兄は弟がQ地点を出発してから何時間後に出発したか求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
ある日、兄と弟2人がP地点からQ地点まで同じ道を歩きました。弟は途中1回だけ速さを変え、兄は一定の速さで進んだところ、兄の方が30分早くQ地点に着きました。弟が速さを変えてから兄に追い抜かれるまでの時間と追い抜かれてから兄がQ地点に着くまでの時間は同じでした。下のグラフはその日に2人が出発してからQ地点に着くまでの時間と道のりを表したものです。

(1) 弟がQ地点に着いたときの速さは、時速何kmか求めなさい。
(2) P地点からQ地点までの距離を求めなさい。
(3) 次の日、弟は(1)の速さでQ地点からP地点まで歩きました。弟が出発した後に兄はQ地点を出発し、前日と同じ速さで歩きました。弟がP地点に着いたときの兄との距離の差は、兄が出発したときの弟との差の$ \displaystyle \frac{5}{11} $倍でした。このとき、兄は弟がQ地点を出発してから何時間後に出発したか求めなさい。(1)
色の付いた2つの三角形は合同となるので、弟は1.1km(=3.6-2.5)を30分で歩いたことになる。よって時速2.2km。
(答え) 時速2.2km
(2)
兄の速さ:時速3km(簡単なので計算省略)
弟の速さ:時速2.2km(50分以降)
追いつき算を使い、50分後から追いつくまでの時間を出す。
1.1=(3-2.2)×追いつくまでの時間
追いつくまでの時間=1.375時間
よって、兄がP地点からQ地点までに掛かる時間は50分+1.375時間×2=$ \displaystyle \frac{43}{12} $時間
P地点からQ地点までの距離=3×$ \displaystyle \frac{43}{12} $=10.75km(答え) 10.75km
(3)
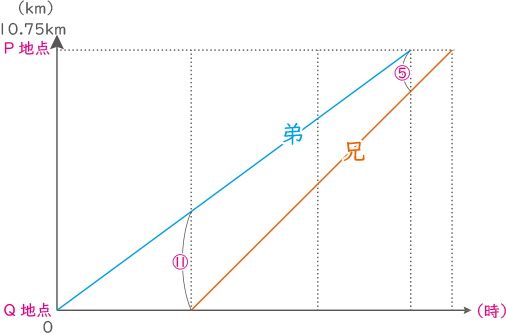
まず、下図のような比⑤:⑪が分かっている。
弟がP地点までにかかる時間は、10.75÷2.2=$ \displaystyle \frac{215}{44} $時間
兄がP地点までにかかる時間は、10.75÷3=$ \displaystyle \frac{43}{12} $時間
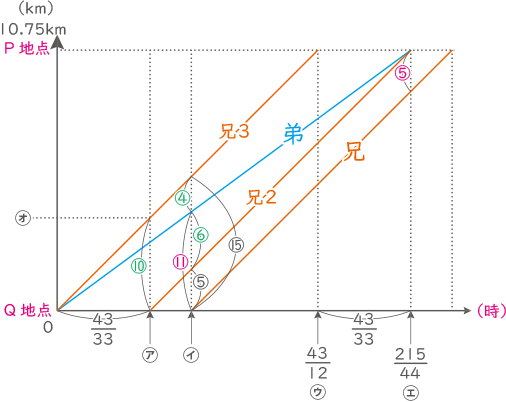
その時間差は$ \displaystyle \frac{43}{33} $時間、さらに兄の線と平行な兄1,兄2の線を追記し、比を求めてゆく。
上図について。
(ⅰ)(㋓-㋒)=$ \displaystyle \frac{44}{33} $=㋐となる。
(ⅱ)㋓の⑤から、㋑にも⑤が見つかる。(合同な三角形があるので。)
(ⅲ)㋑の時刻に兄弟の歩いた距離の比は3:2.2なので3:2.2=⑮:⑪となり、④:⑥:⑤とわかる。
(ⅳ)兄2と兄3は平行なので㋔の距離は④+⑥=⑩とわかる。
(ⅴ)相似な三角形より、㋐($ \displaystyle \frac{44}{33} $):㋑=⑩:⑮となるので㋑を求める。㋑=$ \displaystyle \frac{44}{33} $×$ \displaystyle \frac{15}{10} $=$ \displaystyle \frac{44}{22} $=1$ \displaystyle \frac{21}{22} $
(答え) 1$ \displaystyle \frac{21}{22} $時間後