旅人算-3-2（暁星中学2022/ちょっぴり難しめの旅人算）

問題

解答

 解答を開く

 

太郎君とお父さんが池の周りをジョギングしました。1日目は2人が同じ地点から反対向きに走り、5度目に出会った時に走るのをやめました。2日目は太郎君は1日目と同じ速さで、お父さんは1日目の1割増しの速さで走りました。2人は同じ地点から同じ向きに走り、お父さんが太郎君に追いついた時に走るのをやめました。2人が走った時間は、2日間とも同じでした。

（1） 1日目の太郎君とお父さんの速さの比を求めなさい。
（2） 太郎君が走った距離は、2日間とも3000m でした。池の周りは何m か求めなさい。

 

---

 

（1）
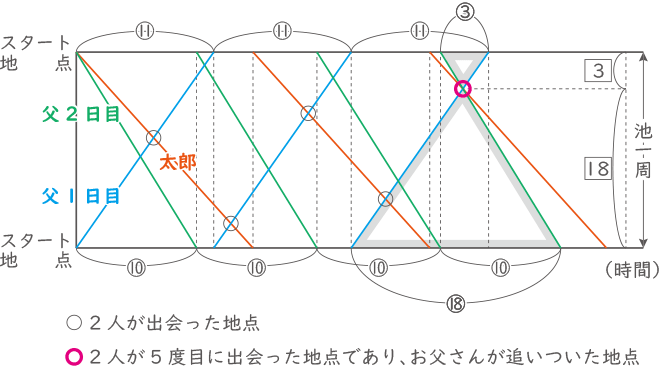
1日目のお父さんの速さを10とすると、2日目のお父さんの速さは11となり、かかる時間は逆比の⑪：⑩になる。これをもとに出来るダイアグラムが下図。

三角形の相似が見つかるので、1日目の太郎君とお父さんの走った距離の比がわかる。
池一周の長さを1とすると、
1日目の太郎君の走った距離＝2＋$ \displaystyle \frac{3}{21} $＝$ \displaystyle \frac{45}{21} $
1日目のお父さんの走った距離＝2＋$ \displaystyle \frac{18}{21} $＝$ \displaystyle \frac{60}{21} $
よって、1日目の太郎君とお父さんの走った距離の比は3：4で、速さと距離は比例するので、1日目の太郎君とお父さんの速さの比も3：4。

（答え）　3：4

 

 別解

面倒なダイヤグラムより式のみで突破したい人はこっち
タ：太郎くんの速さ
ト：1日目のお父さんの速さ
ジ：2人が走った時間
（ト×ジ）＋（タ×ジ）＝池5周・・・㋐
（ト×ジ）×1.1－（タ×ジ）＝池1周・・・㋑
㋑×5
（ト×ジ）×5.5－（タ×ジ）×5＝池5周・・・㋒
㋐と㋒の消去算

（ト×ジ）＋（タ×ジ）＝（ト×ジ）×5.5－（タ×ジ）×5
（タ×$\cancel{ジ}$）×6＝（ト×$\cancel{ジ}$）×4.5
タ×12＝ト×9
タ×4＝ト×3
タ（太郎くんの速さ）：ト（お父さんの速さ）＝3：4

（答え）　3：4

 

（2）
（1）より、池一周の長さを1としたときの1日目の太郎君の走った距離は$ \displaystyle \frac{45}{21} $であり、これが3000mにあたる。
3000÷$ \displaystyle \frac{45}{21} $＝1400

（答え）　1400ｍ