問題
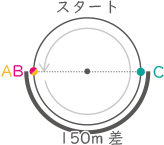
1周300mの池の周りを,A君とB君は同じ地点Xから同時にスタートし,左回り(反時計回り)に走ります。A君は分速200m,B君は分速250mで走りますが,自分の前10m以内に相手がいるときは速さが1.2倍になります。
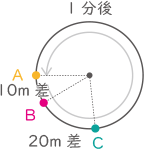
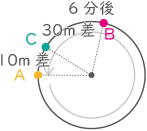
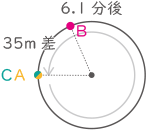
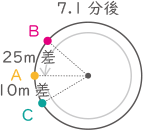
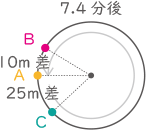
例えば,スタート直後は,A君の前10m以内にB君がいるので,A君は分速240mで走ることになります。一方,B君は分速250mで走ることになります。また,B君が1周分の差をつけてA君に追いつく直前では,B君の前10m以内にA君がいるので,A君は分速200m, B君は分速300mで走ることになります。
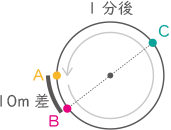
(1) A君とB君が初めて10m離(はな)れるまでに,A君が走る距離(きょり)は何mですか。
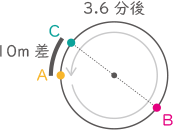
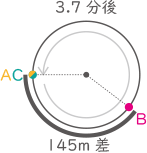
(2) B君がちょうど1周分の差をつけてA君に追いつくまでに,A君が走る距離は何mですか。
(3) A君が10周してスタート地点Xに戻(もど)ってくるまでにかかる時間は何分何秒ですか。
今度は,A君とB君にC君を加えて,3人で池の周りを左回りに走ります。3人は同時にスタートしますが,C君だけはスタートする地点が違(ちが)います。また,C君の走る速さは,B君と同じ分速250mで,3人とも自分の前10m以内に誰(だれ)かがいるときは速さが1.2倍になります。
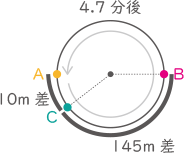
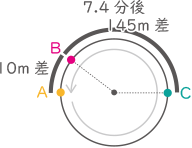
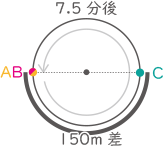
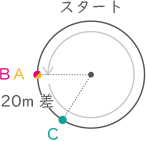
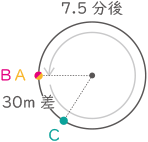
(4) C君のスタートした地点が,他の2人のスタート地点Xから左回りに150mのところでした。
(ア) B君がちょうど1周分の差をつけてA君に追いつくまでに,A君が走る距離は何mですか。
(イ) A君が10周してスタート地点Xに戻ってくるまでの時間は,(3)で求めた時間より何秒短くなりますか。
(5) A君が10周してスタート地点Xに戻ってくるまでの時間が,(3)で求めた時間より7秒短くなりました。また,B君とC君が10m以内に近づくことはありませんでした。このとき,C君がスタートした地点は,他の2人のスタート地点Xから左回りに何mのところでしたか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
1周300mの池の周りを,A君とB君は同じ地点Xから同時にスタートし,左回り(反時計回り)に走ります。A君は分速200m,B君は分速250mで走りますが,自分の前10m以内に相手がいるときは速さが1.2倍になります。
例えば,スタート直後は,A君の前10m以内にB君がいるので,A君は分速240mで走ることになります。一方,B君は分速250mで走ることになります。また,B君が1周分の差をつけてA君に追いつく直前では,B君の前10m以内にA君がいるので,A君は分速200m, B君は分速300mで走ることになります。(1) A君とB君が初めて10m離(はな)れるまでに,A君が走る距離(きょり)は何mですか。
(2) B君がちょうど1周分の差をつけてA君に追いつくまでに,A君が走る距離は何mですか。
(3) A君が10周してスタート地点Xに戻(もど)ってくるまでにかかる時間は何分何秒ですか。
今度は,A君とB君にC君を加えて,3人で池の周りを左回りに走ります。3人は同時にスタートしますが,C君だけはスタートする地点が違(ちが)います。また,C君の走る速さは,B君と同じ分速250mで,3人とも自分の前10m以内に誰(だれ)かがいるときは速さが1.2倍になります。
(4) C君のスタートした地点が,他の2人のスタート地点Xから左回りに150mのところでした。
(ア) B君がちょうど1周分の差をつけてA君に追いつくまでに,A君が走る距離は何mですか。
(イ) A君が10周してスタート地点Xに戻ってくるまでの時間は,(3)で求めた時間より何秒短くなりますか。(5) A君が10周してスタート地点Xに戻ってくるまでの時間が,(3)で求めた時間より7秒短くなりました。また,B君とC君が10m以内に近づくことはありませんでした。このとき,C君がスタートした地点は,他の2人のスタート地点Xから左回りに何mのところでしたか。
(1)
スタート時、AB2人の距離は10m以内なので
A:分速240m(1.2倍)
B:分速250m
1分間で10mの差がつくので、Aの走る距離は240m(答え) 240m
(2)
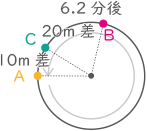
スタートしてから1分後(AB2人は10m離れる)から、BがAに追いつく手前10mまでのAの走る距離
A:分速200m
B:分速250m
(300-10-10)÷(250-200)=5.6分、200×5.6=1120mBがAに追いつく手前の10mから、追いつくまでのAの走る距離
A:分速200m
B:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20mよって、240+1120+20=1380m
(答え) 1380m
(3)
前問よりBがAに追いつくまで、Aは1380m走り、池を1380÷300=4.6周する。倍の2760mでは9.2周することになる。300×0.2=60mより、あと240mで10周になる。この240mは(1)の状況と同じ。
よって、求める時間は(1+5.6+0.1)×2+1=14.4分、14分24秒(答え) 14分24秒
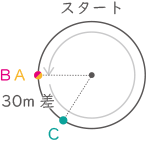
(4)-(ア)
スタート位置

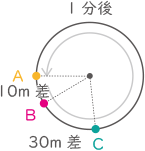
① スタートしてから1分間でAは200×1.2×1=240m進む。
このとき、BCの距離はスタート時と同じで150m
② スタートしてから1分後、AはCの140m前方にいる。そこからCがAの後方10mに追いつくまでにAの走る距離
A:分速200m
C:分速250m
(140-10)÷(250-200)=2.6分、200×2.6=520m
このとき、BCの距離はスタート時と同じで150m
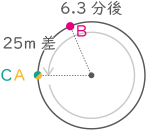
③ CがAの後方10mから追いつくまでにAの走る距離
A:分速200m
C:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20m
このとき、BCの距離は145m(0.1分間だけCがBより分速50m速く走った)
④ CがAを追いこしてから10m差をつけるまでにAの走る距離
A:分速240m(1.2倍)
C:分速250m
10÷(250-240)=1分、240×1=240m
このとき、BCの距離は145mでABの距離は145m
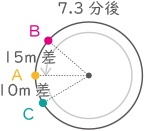
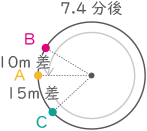
⑤ BがAの後方10mに追いつくまでにAの走る距離
A:分速200m
B:分速250m
(145-10)÷(250-200)=2.7分、200×2.7=540m
このとき、BCの距離は145m
⑥ BがAの後方10mからAに追いつくまでにAの走る距離
A:分速200m
B:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20m
このとき、BCの距離は150m
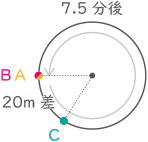
よって、Aは7.5分かけて240+520+20+240+540+20=1580m走る。
(答え) 1580m
(4)-(イ)
(ア)より、Aが1580m走った時は、3人の位置関係はスタート時と同じなので、(ア)の①~⑥をくり返す。
3000(10周)-1580=1420mなので、①240+②520+③20+④240+⑤400(540mの途中)で1420mになり、かかる時間は(1+2.6+0.1+1+2)分。1周目の7.5分と合わせ14.2分(14分12秒)。
よって、(3)より12秒短くなる。(答え) 12秒短くなる
(5)
7秒短くなると14分17秒。これを(4)-(イ)の14分12秒と比較すると5秒長く(遅く)なっている。
遅くするには、2回目にAが毎分240mで走る区間((4)-(ア)の④)の一部または全部を3000mよりも後にすればよく、そのためには、毎分200mで走る区間((4)-(ア)の②)をできるだけ多くとる。(地点Xにできるだけ近づける。)
よって、CB間が10mより開いていて、かつ計算の簡単な数値「地点Xから左に20m」で計算し、結果が14分17秒より遅ければ「地点Xから左に30m」、速ければ「地点Xから左に15m」を計算し、つるかめ算的に求める。【地点Xから左に20m】
スタート位置

① スタートしてから1分間でAは200×1.2×1=240m進む。
このとき、BCの距離はスタート時と同じで20m
② スタートしてから1分後、AはCの270m前方にいる。そこからCがAの後方10mに追いつくまでにAの走る距離
A:分速200m
C:分速250m
(270-10)÷(250-200)=5.2分、200×5.2=1040m
このとき、BCの距離はスタート時と同じで20m
③ CがAの後方10mから追いつくまでにAの走る距離
A:分速200m
C:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20m
このとき、BCの距離は25m(0.1分間だけCがBより分速50m速く走った)
④ CがAを追いこしてから10m差をつけるまでにAの走る距離
A:分速240m(1.2倍)
C:分速250m
10÷(250-240)=1分、240×1=240m
このとき、BCの距離は25mでABの距離は15m
⑤ BがAの後方10mに追いつくまでにAの走る距離
A:分速200m
B:分速250m
(15-10)÷(250-200)=0.1分、200×0.1=20m
このとき、BCの距離は25m
⑥ BがAの後方10mからAに追いつくまでにAの走る距離
A:分速200m
B:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20m
このとき、BCの距離は20m
よって、Aは7.5分かけて240+1040+20+240+20+20=1580m走り、その時の3人の位置関係はスタート時と同じ。
Aが残り1420m走れば3000m(10周)になるので2周目の途中で3000mになる。
1420=240(①)+1040(②)+20(③)+120(④の半分で0.5分間走る)にかかる時間と7.5分で、(1+5.2+0.1+0.5)分+7.5分=14.3分=14分18秒。14分17秒より遅くなったので次は「地点Xから左に30m」を計算する。
【地点Xから左に30m】
スタート位置

① スタートしてから1分間でAは200×1.2×1=240m進む。
このとき、BCの距離はスタート時と同じで30m
② スタートしてから1分後、AはCの260m前方にいる。そこからCがAの後方10mに追いつくまでにAの走る距離
A:分速200m
C:分速250m
(260-10)÷(250-200)=5分、200×5=1000m
このとき、BCの距離はスタート時と同じで30m
③ CがAの後方10mから追いつくまでにAの走る距離
A:分速200m
C:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20m
このとき、BCの距離は35m(0.1分間だけCがBより分速50m速く走った)
④ CがAを追いこしてから10m差をつけるまでにAの走る距離
A:分速240m(1.2倍)
C:分速250m
10÷(250-240)=1分、240×1=240m
このとき、BCの距離は35mでABの距離は25m
⑤ BがAの後方10mに追いつくまでにAの走る距離
A:分速200m
B:分速250m
(25-10)÷(250-200)=0.3分、200×0.3=60m
このとき、BCの距離は35m
⑥ BがAの後方10mからAに追いつくまでにAの走る距離
A:分速200m
B:分速300m(1.2倍)
10÷(300-200)=0.1分、200×0.1=20m
このとき、BCの距離は30m
よって、Aは7.5分かけて240+1000+20+240+60+20=1580m走り、その時の3人の位置関係はスタート時と同じ。
Aが残り1420m走れば3000m(10周)になるので2周目の途中で3000mになる。
1420=240(①)+1000(②)+20(③)+160(④の$ \displaystyle \frac{2}{3} $で40秒間走る)にかかる時間と7.5分で、(1+5+0.1)分+40秒+7.5分=13.6分+40秒=14分16秒。「地点Xから左に20m」では14分18秒で、「地点Xから左に30m」では14分16秒となり、この間の速さは一定なので中間の「地点Xから左に25m」が14分17秒になる。
(答え) 地点Xから左に25mのところ