問題
K学園自転車同好会のA君とB君の2人は,1周が8kmの円形のコースをS地点から自転車でスタートして,A君はコースを反時計回りに時速36kmで,B君はコースを時計回りに時速28kmで走り,2人ともコースを6周してS地点に戻ってくることにしました。走り終わったらすぐにコースから外れるものとして次の【 】を埋めなさい。
スタートしてから二人とも走り終わるまでに二人は【あ】回すれ違います。このとき,A君は最後の2周でB君と【い】回すれ違い,B君は最後の2周でA君と【う】回すれ違います。B君は4周目の走行中にA君と【え】回すれ違いますが,そのうちでA君も4周目を走行していたときにすれ違った地点をTとすると,S地点からT地点までの近い方の道のりは【お】kmです。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
K学園自転車同好会のA君とB君の2人は,1周が8kmの円形のコースをS地点から自転車でスタートして,A君はコースを反時計回りに時速36kmで,B君はコースを時計回りに時速28kmで走り,2人ともコースを6周してS地点に戻ってくることにしました。走り終わったらすぐにコースから外れるものとして次の【 】を埋めなさい。
スタートしてから二人とも走り終わるまでに二人は【あ】回すれ違います。このとき,A君は最後の2周でB君と【い】回すれ違い,B君は最後の2周でA君と【う】回すれ違います。B君は4周目の走行中にA君と【え】回すれ違いますが,そのうちでA君も4周目を走行していたときにすれ違った地点をTとすると,S地点からT地点までの近い方の道のりは【お】kmです。
【あ】
S地点から最初に出会う地点までにかかる時間。
8÷(36+28)=$ \displaystyle \frac{1}{8} $時間
早い方のA君が6周する時間。
8×6÷36=$ \displaystyle \frac{4}{3} $時間
$ \displaystyle \frac{4}{3} $時間の間にすれ違う回数。
$ \displaystyle \frac{4}{3} $÷$ \displaystyle \frac{1}{8} $=10あまり2(答え) 10回
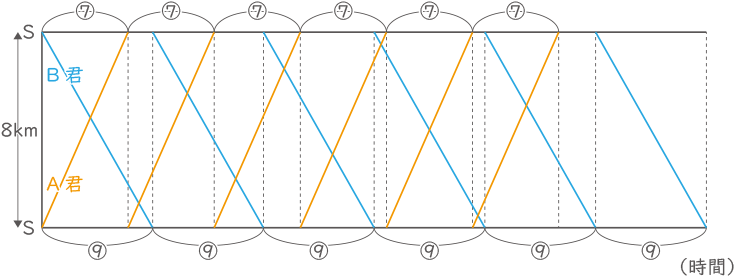
A君とB君の1周する時間比は速さの逆比より⑦:⑨となり、これを使ってダイヤグラムを作る。
(今回は計算で求めるよりもダイヤグラムを作る方が圧倒的に楽。)
【い】
図より、3回。(答え) 3回
【う】
図より、1回。(答え) 1回
【え】
図より、3回。(答え) 3回
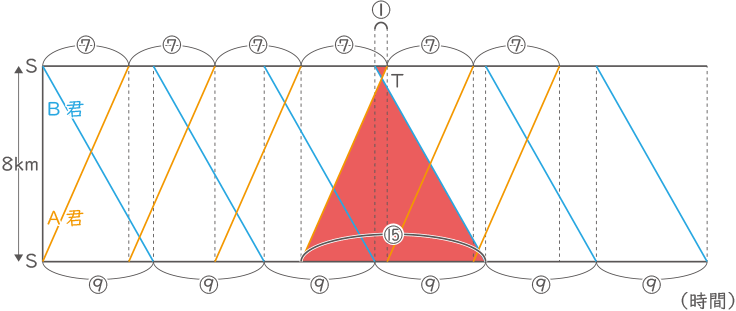
【お】

図の様に相似な三角形を見つけ、①:⑮の比を利用してS地点からT地点までの距離を求める。
8×$ \displaystyle \frac{①}{⑯} $=0.5km。(答え) 0.5km