問題
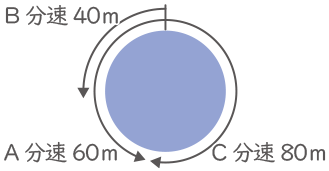
Aさん、Bさん、Cさんが池の周りを同じ地点から同時に回りだします。Aさんは分速60m、Bさんは分速40mで2人とも左回りに、Cさんは分速80mで右回りに進みます。AさんとCさんは12分後に出会います。
(1)池の周りは何mですか。
(2)BさんとCさんは何分後に出会いますか。
(3)AさんはBさんを何分後に追いこしますか。
(4)3人が初めて同時にもとの場所に来るのは何分後ですか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
Aさん、Bさん、Cさんが池の周りを同じ地点から同時に回りだします。Aさんは分速60m、Bさんは分速40mで2人とも左回りに、Cさんは分速80mで右回りに進みます。AさんとCさんは12分後に出会います。
(1)池の周りは何mですか。
(2)BさんとCさんは何分後に出会いますか。
(3)AさんはBさんを何分後に追いこしますか。
(4)3人が初めて同時にもとの場所に来るのは何分後ですか。
(1)
AさんとCさんが出会った時が1周した時なので(60+80)×12=1680m(出会い算)
(答え)1680m
(2)
1周1680mをBさんとCさんの速さの和で割る。1680÷(40+80)=14分後(出会い算)(答え)14分後
(3)
AさんBさんの速さを分速40mずつ引くと、Bさんは動かずにAさんだけが分速20mで動いていることになる。Aさんは1680÷(60-40)=84分毎にBさんを追いこすことになる。(答え)84分後
(4)
Aさん、Bさん、Cさんはそれぞれ28分、42分、21分で池を一周するので、その最小公倍数が3人が同時にもとの場所に来るときとなる。
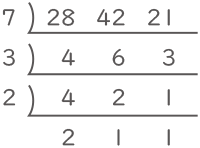
すだれ算(連除法)で最小公倍数を求めると、7×3×2×2=84分後となる。
(答え)84分後