問題
A地点とB地点は1200m離れており、甲君はA地点から、乙君はB地点から何度も2地点間を往復します。甲君は分速80m、乙君は分速240mで同時に動き出した時、初めて二人が出会うのはA地点から(ア)mのところで、その後、乙君は一度目のA地点に着きますが、それは動き出してから(イ)分後です。さらに、A地点から折り返した乙君が初めて甲君に追い付くのは動き出してから(ウ)分後です。また、2人が2度目に出会うのは動き出してから(エ)分後です。
(ア)、(イ)、(ウ)、(エ)を求めなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
A地点とB地点は1200m離れており、甲君はA地点から、乙君はB地点から何度も2地点間を往復します。甲君は分速80m、乙君は分速240mで同時に動き出した時、初めて二人が出会うのはA地点から(ア)mのところで、その後、乙君は一度目のA地点に着きますが、それは動き出してから(イ)分後です。さらに、A地点から折り返した乙君が初めて甲君に追い付くのは動き出してから(ウ)分後です。また、2人が2度目に出会うのは動き出してから(エ)分後です。
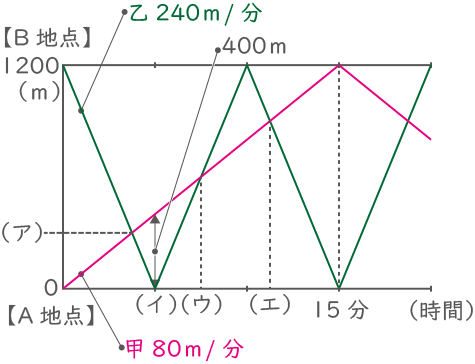
(ア)、(イ)、(ウ)、(エ)を求めなさい。ダイヤグラムを利用する。

(ア)
2人の距離は1200mなので、1200÷(80+240)=3.75分後(2人の速さの和を使う出会い算)に出会い、そこはA地点から80×3.75=300mのところとなる。(答え)300
(イ)
1200÷240=5分(答え)5
(ウ)
(イ)は2人が動き出してから5分後で、その時、甲君は80×5=400m進み、乙君はA地点にいる。2人は400m離れているので、(イ)の時間から400÷(240-80)=2.5分後(2人の速さの差を使う追いつき算)に同じ地点になる。動き出してからは5+2.5=7.5分後。(答え)7.5
(エ)
15分後に甲君はB地点に、乙君はA地点にいる。15分後をスタート位置として、2人の動きを逆再生させると出会い算で簡単に解ける。計算は(ア)と同じことなので15分後より3.75分前に2人は2度目の出会いをすることになる。動き出してから15-3.75=11.25分後。(答え)11.25
ポイントダイヤグラム必須。ダイヤグラムを精密に書くとそれだけでかなり分かることが出てくる。